Lecture 04: Introduction to MoE
随着2025年春节DeepSeek-R1 的发布,Mixture of Experts (MoE) 模型在自然语言处理领域重新引起了广泛关注。这节课我们将会学习什么的MoE Layer。它的基本原理是什么?它是如何工作的?以及它为什么能够提升模型的性能。
在Assignment01中,我们实现了FFN Layer。但是作业中并没有要求大家实现MoE Layer。为了帮助大家更好地理解MoE Layer的实现细节,也作为大家关注我的Bonus,我在Assignment01的代码库中添加了MoE Layer的实现代码。大家可以参考以下链接查看代码实现。
我们首先来了解一下,什么是Mixture of Experts (MoE) 模型,并且为什么它受到了如此多的关注。
1 What is Mixture of Experts (MoE)?
过去几年,大模型的主流路线几乎只有一条:把 Transformer 做得更大、更深、更宽,然后用更多数据与更多算力堆上去。Mixture of Experts(MoE)的出现,给这条路线增加了一个非常“工程味”的分支:在不显著增加每一步计算量(FLOPs)的前提下,把模型的参数容量做得更大。
在这里需要提一点的是,MoE中的“专家”(Expert)指的是模型中的一个子网络,通常是一个独立的神经网络层或模块。而并不是模型里真的存在“代码专家 / 英语专家 / 数学专家”。
如果你把大模型训练理解为“在固定预算下换取最强效果”,那 MoE 之所以引发关注,核心就一句话:
同样的训练/推理 FLOPs,MoE 往往能给你更低的 loss、更好的 perplexity、更好的下游表现——只要你能把它训练稳、跑得快。
这也解释了为什么 MoE 在 2024–2025 迅速从“研究圈的技巧”变成“工业界的默认选项”之一.
其实MoE的概念并不新鲜,比如 Switch Transformer (Fedus, Zoph, and Shazeer 2022) 早在2021年就提出,并且改进了MoE的训练稳定。我们先来看一下MoE的基本结构。
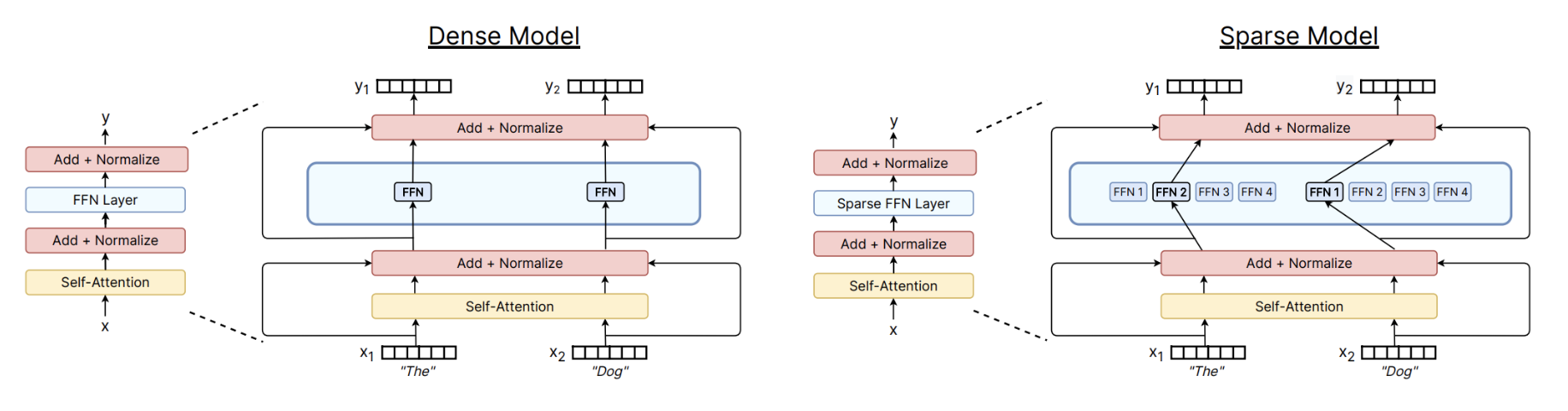
从 Figure 1 中可以看出,每个token被送入其中一个专家网络(Expert)进行处理,而不是像传统的FFN Layer那样,所有token都经过同一个FFN Layer。这样一来,MoE Layer的参数量可以大幅增加,而每个token实际计算的FLOPs并没有显著增加。
在相等的FLOPs下,参数量的增加,往往能带来模型表达能力的提升,从而提升模型的性能。这也是MoE能够在不显著增加计算量的前提下,提升模型性能的原因之一。
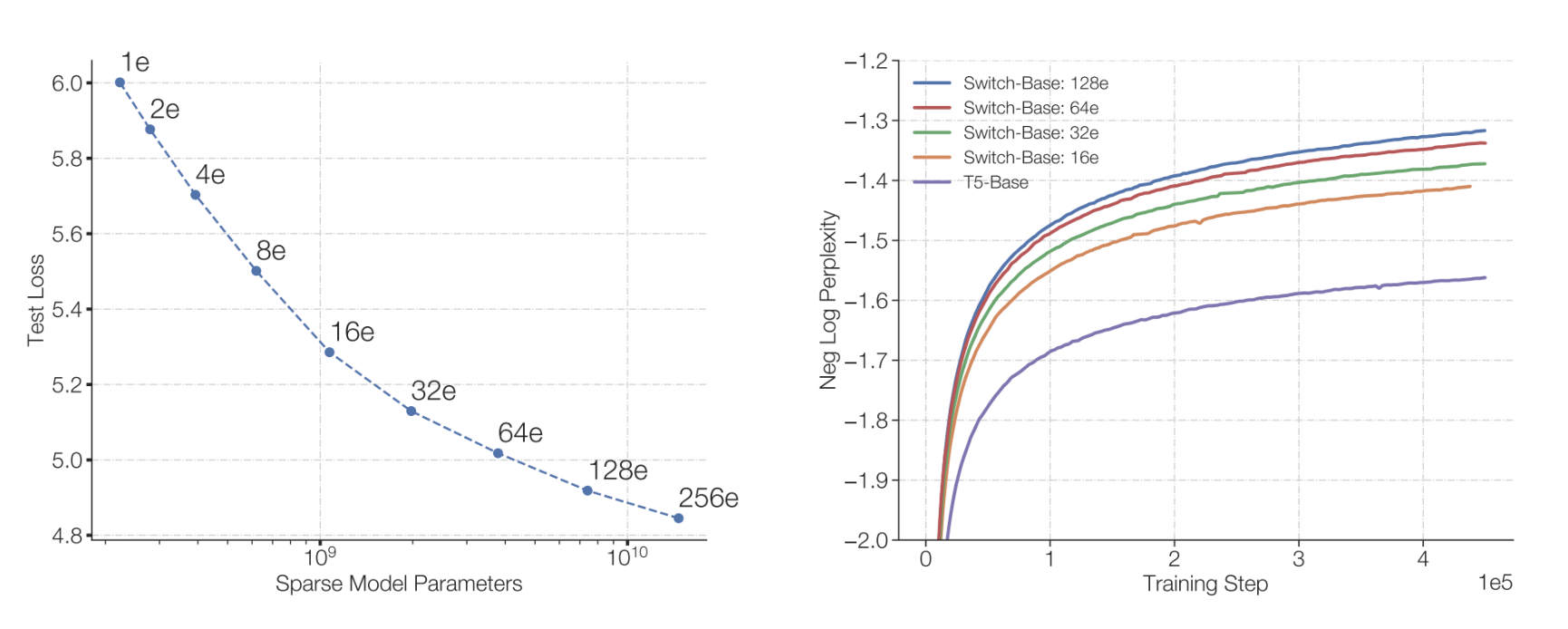
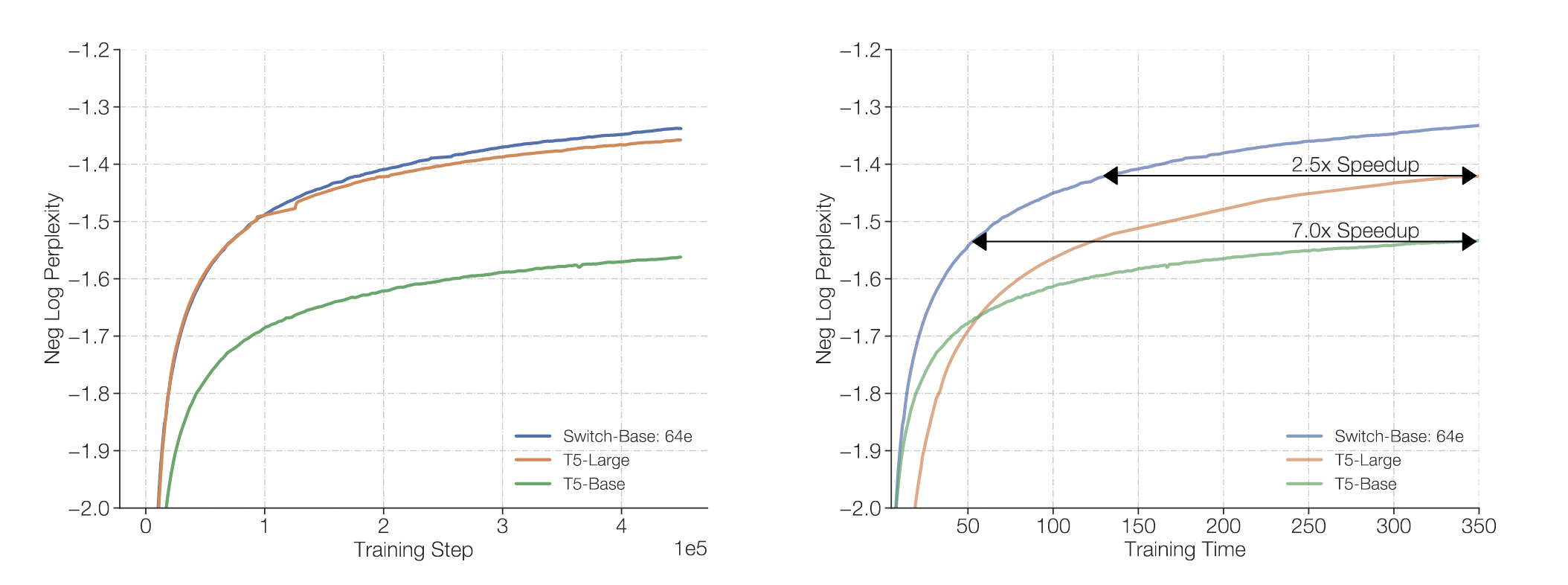
另外一个优点就是了, MoE所需的训练时间更短。如下图所示,在达到相同的perplexity水平下,MoE模型所需的训练时间明显少于Dense模型。
并且,由于MoE有不同的Experts, 并且每个Expert可以独立训练,这使得MoE模型在分布式训练中更具优势。我们可以将不同的Experts分配到不同的计算节点上,从而更好地利用分布式计算资源,提高训练效率。
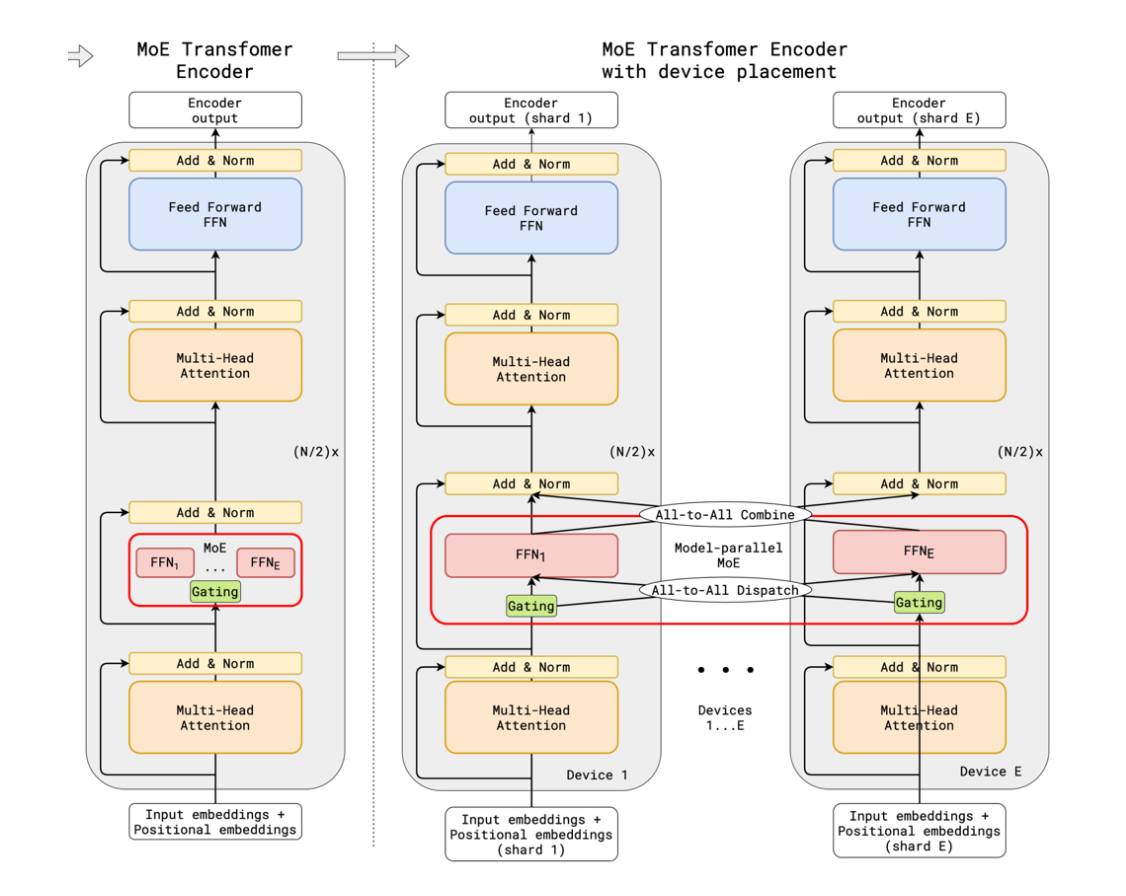
但是,既然MoE有这么多优点,为什么它不是大模型的唯一选择呢?这就要提到MoE的几个挑战了。
- 训练稳定性:由于MoE模型中有多个Experts,如何确保每个Expert都能得到足够的训练数据是一个挑战。如果某些Experts很少被选择,可能会导致它们无法有效学习,从而影响整体模型的性能。
- 路由机制:MoE模型需要一个路由机制来决定每个token应该送入哪个Expert。设计一个高效且有效的路由机制是MoE模型的关键之一。
- 实现复杂性:MoE模型的实现相对于传统的Dense模型更为复杂,尤其是在分布式训练环境下,需要处理更多的通信和同步问题。
正是由于这些挑战,MoE模型在实际应用中需要更多的工程技巧和经验。因此,虽然MoE有很多潜在的优势,但它并不是适合所有场景的万能解决方案。
TL;DR
MoE 之所以火,是因为它把 Transformer 里最“贵”的 FFN 变成很多个专家,但每次只激活少数几个:在 FLOPs 近似不变的情况下显著增加参数容量,通常能带来更好的训练/推理性价比;代价是训练稳定性与系统实现复杂度。
了解了MoE的基本概念,优点和挑战后,接下来我们将深入探讨MoE的具体实现细节,包括路由机制、训练方法等内容。
2 MoE Architecture
在第一节我们意见了解了MoE的基本概念以及基本的架构 Figure 1,在这一节我们将更详细地介绍MoE的架构组成部分,包括:
- Routing Function: 决定每个token应该送入哪个Expert的函数。
- Experts :多个独立的FFN Layer,每个Expert负责处理一部分token。
- Training Objectives:MoE模型的训练目标和损失函数设计。
首先,我们来看一下Routing Function的设计。
2.1 Routing Function
MoE 的核心不是“有很多专家”,而是每个 token 该去哪些专家。这个决策由 Router(路由器)完成。我们可以把它理解成一个“轻量的分类器/打分器”:输入是每个 token 的 hidden state,输出是对所有专家的偏好分数,然后选出 top-K 个专家执行。有一点很重要的是:
Router 是具有上下文感知能力的,也就是说它会根据 token 的内容动态决定路由结果,也就是说同一个 token 在不同语境下可以被送去不同专家。
Router实现大概有3种思路:
- Token-choice(token 选专家): 每个 token 给所有专家打分,选择 top-K 专家处理它(现代主流)
- Expert-choice(专家选 token): 每个专家从一批 token 里挑 top-K 个来处理(天然更均衡)
- Global assignment(全局分配):把 token–expert 匹配视作优化问题(如线性分配/最优传输),追求更均衡或更低通信成本
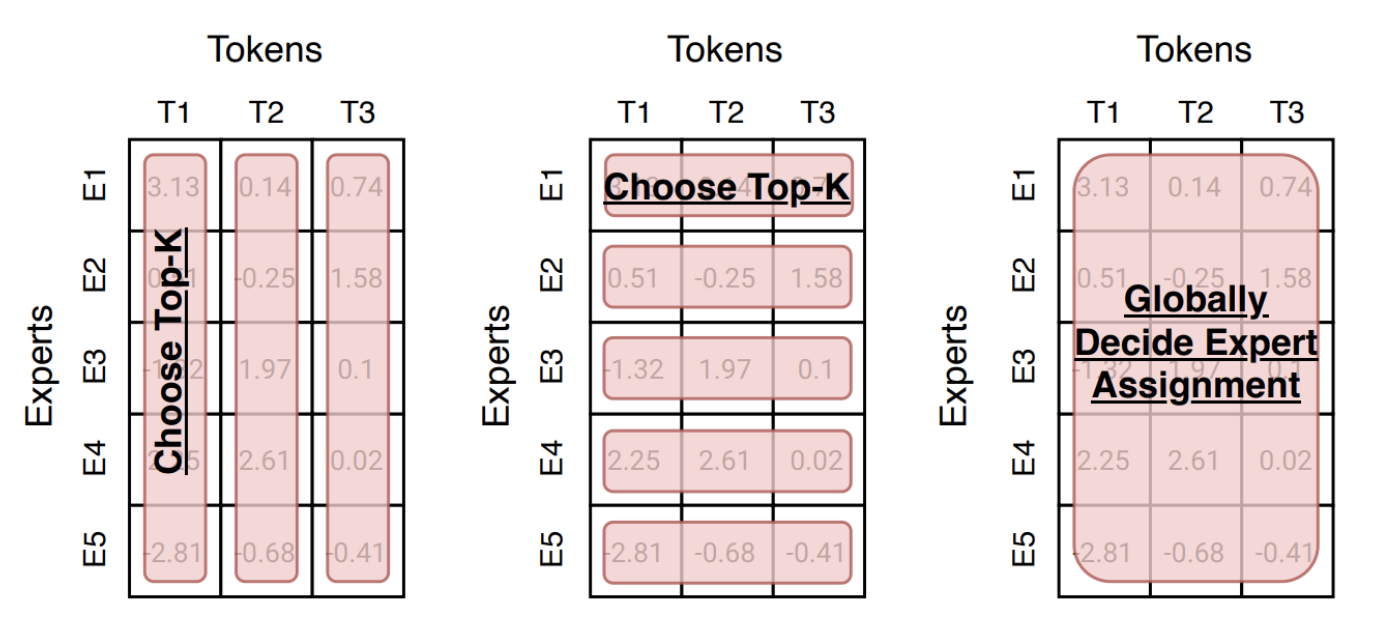
在实际应用中,Token-choice 是目前最主流的设计思路,因为它实现简单且易于扩展。下面我们来看一下Token-choice Router的具体实现。
2.1.1 Token-choice Router
Token-choice Router, 顾名思义,就是每个 token 给所有专家打分,选择 top-K 专家处理它。当然,这个“打分”过程(Routing)可以有很多种实现方式,比如:
- Top-K Gating:使用一个线性层对 token 的 hidden state 进行投影,得到每个专家的分数,然后选择 top-K 个专家。
- Hashing-based Routing:使用哈希函数将 token 映射到专家,从而实现路由(通常作为Baseline)。
- RL to learn Routing:使用强化学习方法来学习路由策略。
- Solve a Optimization Problem:将路由问题视作一个优化问题,通过求解该问题来确定路由结果。
下图展示了不同的Token-choice Router实现方式。
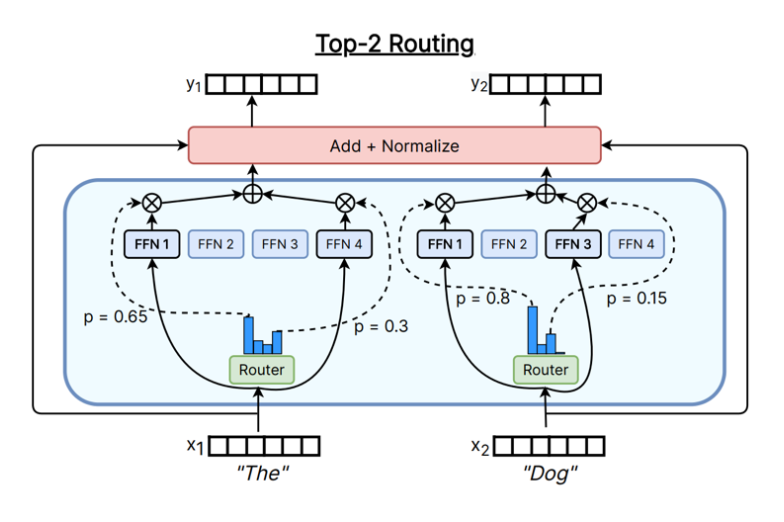
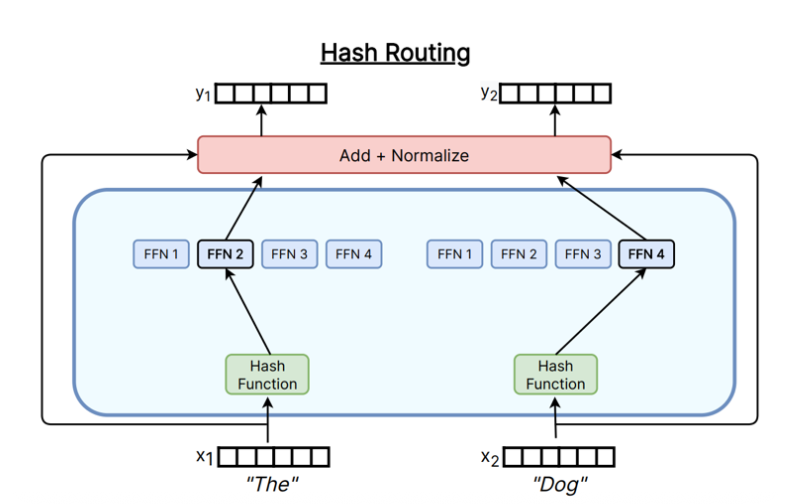
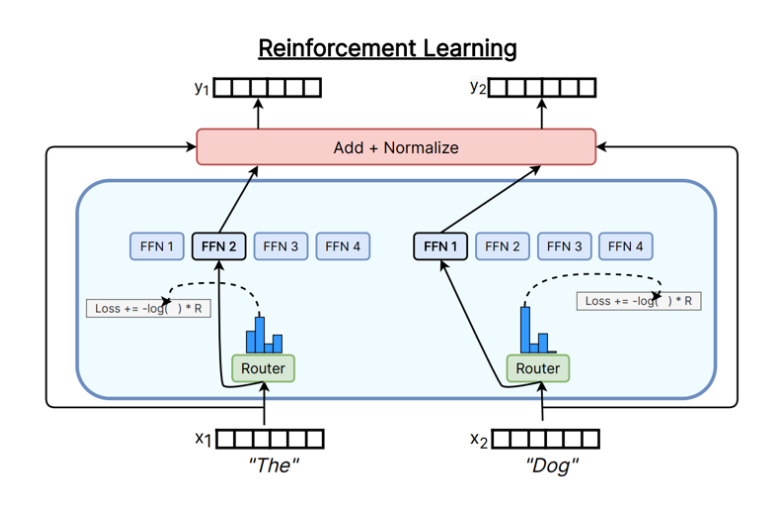
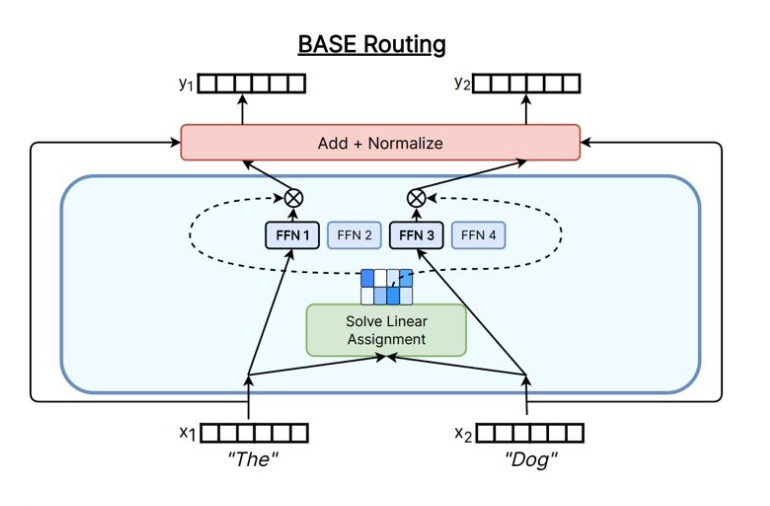
在实际应用中,Top-K Gating 是目前最常用的 Token-choice Router 实现方式,因为它简单且高效。下面我们来看一下 Top-K Gating 的具体实现细节。
2.1.1.1 Top-K Gating
Top-K Gating 的实现步骤如下:
- Score Calculation:对于每个 token 的 hidden state \(h_i\),通过一个线性层计算每个专家的分数: \[ s_{i,j} = W_g h_i + b_g \tag{1}\] 其中,\(W_g\) 和 \(b_g\) 是路由器的参数,\(s_{i,j}\) 是 token \(i\) 对专家 \(j\) 的分数。
有了score之后,接下来我们需要选择 top-K 个专家,不过在此之前,我们通常会对score进行归一化处理,以便更好地比较不同专家的分数。常用的方法是使用softmax函数: \[ p_{i,j} = \frac{exp(s_{i,j})}{\sum_{k} exp(s_{i,k})} \tag{2}\] 其中,\(p_{i,j}\) 是 token \(i\) 对专家 \(j\) 的归一化分数。
Top-K Selection:对于每个 token,选择分数最高的 K 个专家: \[ g_{i, j} = \begin{cases} s_{i, j}, \quad s_{i, j} \in \text{Top-K}(s_i) \\ 0, \quad \text{otherwise} \end{cases} \tag{3}\] 其中,\(g_{i,j}\) 是 token \(i\) 对专家 \(j\) 的选择结果。
Passing to Experts:将 token 送入选择的专家进行处理。每个专家只处理被选中的 token,其余 token 被忽略。
Combining Outputs:将专家的输出进行合并,得到最终的 token 表示。通常使用加权平均的方式: \[ h_i' = \sum_{j} g_{i,j} \text{Expert}_j(h_i) + h_i \tag{4}\] 其中,\(h_i'\) 是 token \(i\) 的最终表示,\(\text{Expert}_j(h_i)\) 是专家 \(j\) 对 token \(i\) 的处理结果, \(h_i\) 是 token \(i\) 的原始表示(Residual Connection), \(g_{i,j}\) 是 token \(i\) 对专家 \(j\) 的选择结果。
通过以上步骤,Top-K Gating 实现了对 token 的动态路由,使得每个 token 只经过少数几个专家,从而实现了 MoE 的高效计算。
2.1.1.2 Top-K Variants
在实际应用中,Top-K Gating 有一些变体,其中比较常见的是DeepSeek提出的Top-K变形(Dai et al. 2024), 它提出,在选择Top-K专家的基础上,每个token还会固定传入一个Shared Expert。这样做的好处是,可以确保每个token至少有一个专家能够处理它。 并且Expert的大小变小,但是数量变多(fine-grained Experts),从而提升模型的表达能力。
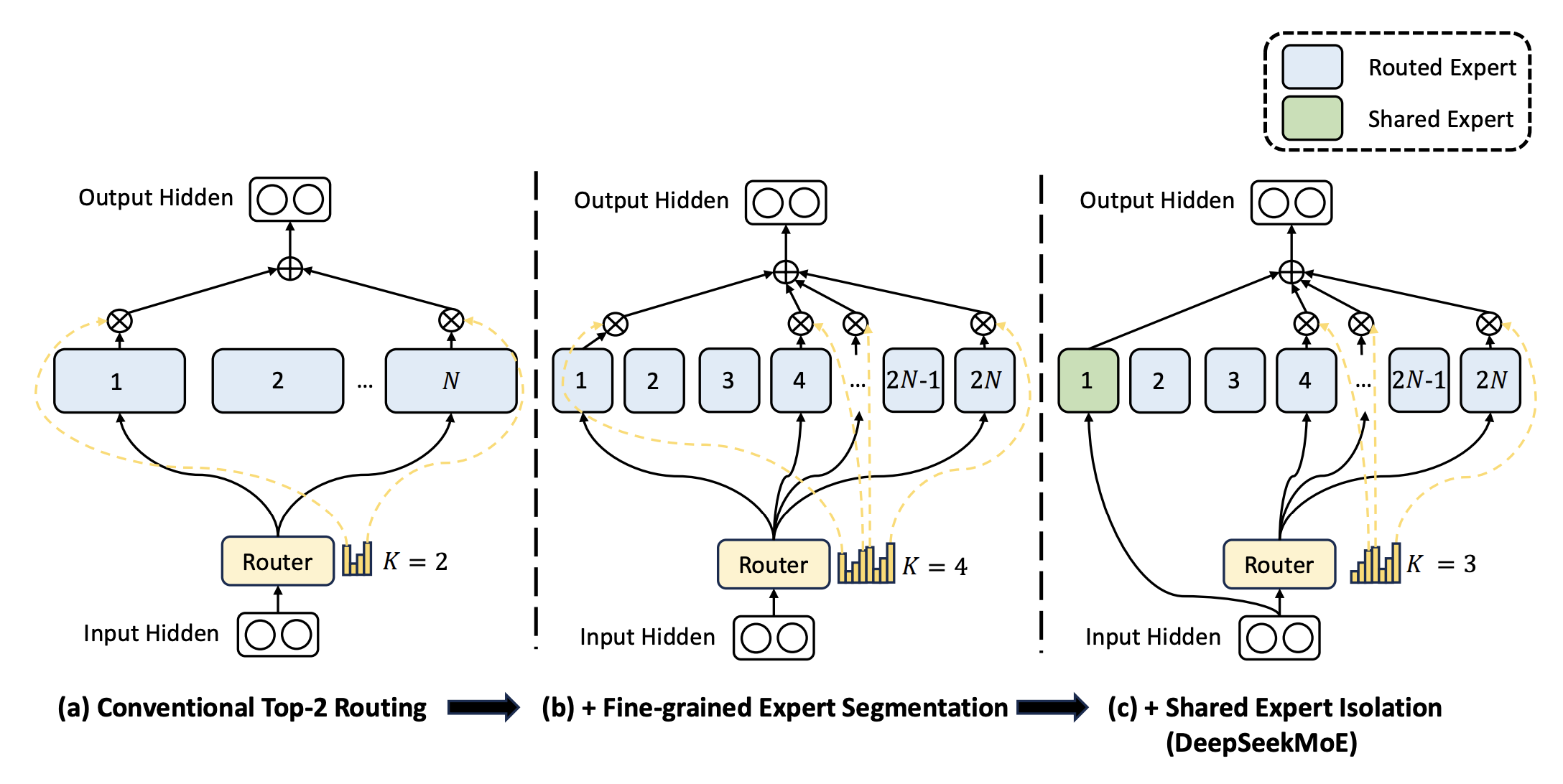
这种方式,在之后的实验中也被证明是有效的。 Qwen3模型(Yang et al. 2025) 也采用了类似的设计。
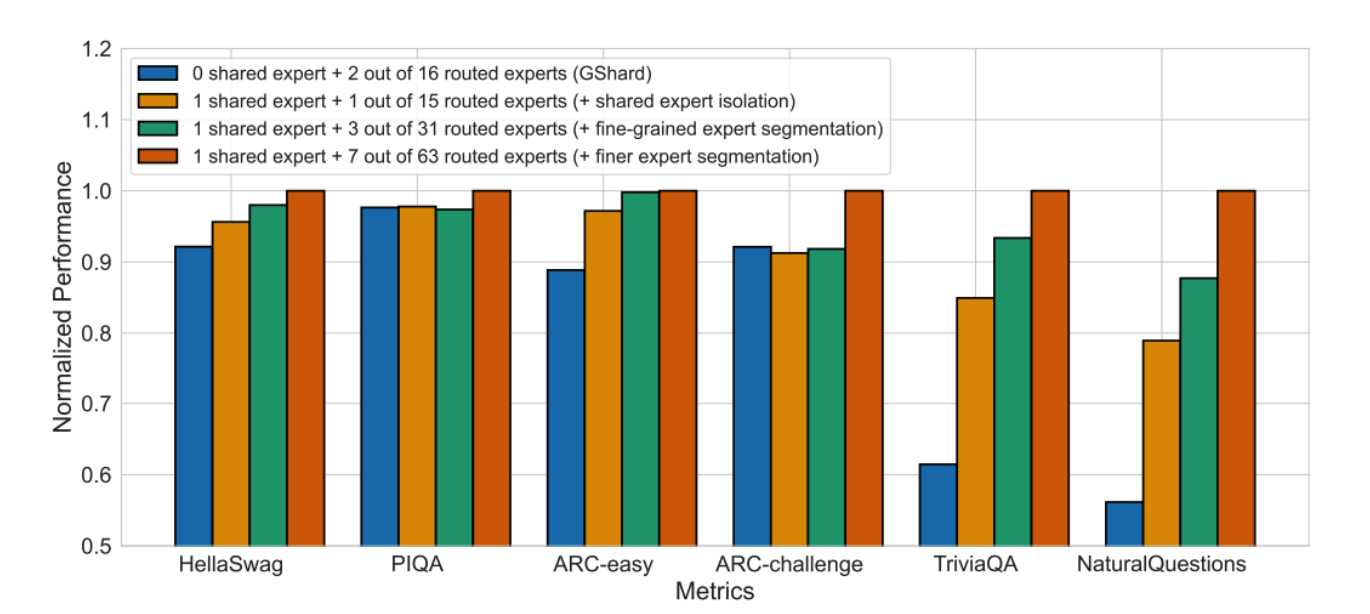
2.1.1.3 Choice of K
我们了解了Top-K Gating的实现细节,接下来我们来看一下K值的选择对模型性能的影响。 K值的选择对MoE模型的性能有显著影响。一般来说,较小的K值可以减少计算量,但可能会限制模型的表达能力;而较大的K值则可以提升模型的表达能力,但会增加计算量。因此,在实际的应用中,通常使用 K=1 或 K=2 作为默认选择。
课堂中有提到,K > 1 时。我们可以把它想象成Bandit的问题(熟悉Reinforcement Learning的同学应该了解)。每个token在选择专家时,就像是在玩一个多臂老虎机(Multi-armed Bandit),每次选择K个专家进行尝试,从而获得更好的奖励(模型性能)。这也是RL中探索与利用(Exploration vs. Exploitation)问题的一个体现。
2.1.1.4 Is Top-K Gating Optimal?
我们了解了Top-K Gating的实现,那么它是不是最优的呢?其实也不尽然。Lecture中有提到一个比较有趣的观察:即使 router 很弱(比如基于 hashing 的确定性映射),很多时候也能比 dense 更强。有一种合理的解释是:只要映射是确定性的,每个专家仍会长期看到某个子分布,从而形成某种“专门化”(不一定是你以为的语义专门化,可能是频率/模式上的专门化)。因此,Router并不一定要设计的很复杂,简单有效即可,这也就是为什么Top-K Gating能这么受欢迎的原因之一。
2.2 Experts
在MoE模型中,Experts是多个独立的FFN Layer,每个Expert负责处理一部分token。每个Expert通常由一个前馈神经网络(Feed-Forward Neural Network, FFN)组成,结构与传统的Transformer中的FFN类似,但参数是独立的。那么,Experts的中间层的维度应该如何选择呢? 一般来说,Experts的中间层维度通常设置为输入维度的4倍(即\(4d_{model}\)),和传统的FFN Layer保持一致。这是因为较大的中间层维度可以提升模型的表达能力,从而提升整体性能。 但是,在Figure 7中,我们看到DeepSeek介绍了Fine-Grained Experts的概念,即通过增加Experts的数量,同时减少每个Expert的中间层维度,从而提升模型的表达能力。在DeepSeek MoE 中(Dai et al. 2024), 每个Expert的中间层维度被设置为\(\frac{1}{4}d_{ff}\). 这样做的好处是,可以让模型拥有更多的专家,从而提升模型的多样性和表达能力。
DeepSeekMoE has 1 shared expert and 63 routed experts, where each expert is 0.25 times the size of a standard FFN. DeepSeekMoE: Towards Ultimate Expert Specialization in Mixture-of-Experts Language Models, p.9
2.3 Training Objectives
如果说 Routing Function 解决的是“每个 token 去哪些专家”,那 Training Objectives 解决的是更现实的问题:“每个专家到底学什么”。在 MoE 里,单纯靠主任务 loss(Next token Prediction Loss) 往往不够.如果你只用语言模型的主损失(next-token loss)去训 MoE,router 很容易把所有 token 都送去同一个专家。结果是:一个专家变成“万能专家”,其它专家几乎从不被激活(dead experts),你白白存了一堆参数,性能也会变差。
因此,课堂上也在反复强调的一点是:
MoE 的 forward 很简单,难点在于训练时如何避免 expert collapse,并让专家使用更均匀、更有效率。
接下来,我们来看看这个训练问题难在哪里,以及有哪些常用的解决方法。
2.3.1 The Challenge of MoE Training
MoE 的优势在于,在训练时,我们只需要根据Router来选择激活部分(Top-k)专家进行计算,而不是所有专家都参与计算。这种稀疏激活的方式,可以大幅减少每一步的计算量(FLOPs),从而提升训练效率。但是,这种稀疏激活的方式也带来的挑战是:Top-K是不可微的,这使得我们无法直接使用梯度下降法来优化模型参数。因此,研究员们提出了几种方法来解决这个问题。
2.3.1.1 RL Based Optimization
一种思路是使用强化学习(Reinforcement Learning, RL)的方法来优化路由器的参数。
对于不熟悉强化学习的同学,简单介绍一下。强化学习是一种机器学习方法,它通过与环境的交互来学习最优策略。在强化学习中,智能体(Agent)通过观察环境状态(State),选择动作(Action),并根据环境反馈的奖励(Reward)来调整策略,从而最大化累积奖励。 在交互的过程中,Agent所产生的动作通常是离散的(Discrete Action),这就导致了强化学习中的一个核心问题:如何在离散动作空间中进行有效的策略优化。常用的方法包括策略梯度(Policy Gradient)和Q-learning等。 因此,我们可以将MoE的路由问题视作一个强化学习问题,通过设计合适的奖励函数,来引导路由器学习更优的路由策略。
但是,强化学习的方法通常比较复杂,且训练过程不稳定(Gradient Estimation Variance较大),因此在实际应用中并不常用。
2.3.1.2 Stochastic Approximation
另一种思路是使用随机近似(Stochastic Approximation)的方法来优化路由器的参数。具体来说,在 router 打分(logits)里注入噪声/扰动,让 top-K 的选择在训练早期“偶尔换路”,从而更像 bandit 的探索策略。其中一个经典的例子就是 Stochastic Jittering. 它通过在路由器的打分中添加高斯噪声,从而实现对专家的随机选择。接下来我们来看一下Stochastic Jittering的具体实现细节。
2.3.1.2.1 Stochastic Jittering
Stochastic Jittering 的实现步骤如下:
- Router 计算:对于每个 token 的 hidden state \(h_i\),通过一个线性层计算每个专家的分数: \[ s_{i,j} = W_g h_i + b_g \tag{5}\]
- 添加噪声:在每个专家的分数中添加高斯噪声: \[ \tilde{s}_{i,j} = s_{i,j} + \epsilon_{i,j}, \quad \epsilon_{i,j} \sim \mathcal{N}(0, \sigma(x_i)^2) \tag{6}\]
- Top-K 选择:对于每个 token,选择添加噪声后的分数最高的 K 个专家: \[ g_{i, j} = \begin{cases} \tilde{s}_{i, j}, \quad \tilde{s}_{i, j} \in \text{Top-K}(\tilde{s}_i) \\ 0, \quad \text{otherwise} \end{cases} \tag{7}\]
其中,\(\sigma(x_i)\) 是噪声的标准差, 它是一个可学习的函数,通常通过一个小的神经网络来实现。通过调整噪声的大小,可以控制路由器的探索程度,从而提升模型的训练效果。
那么这个Stochastic Jittering解决了什么问题呢? 它其实解决了类似于“探索与利用”(Exploration vs. Exploitation)的问题。在MoE的训练过程中,我们希望路由器能够既能利用当前的知识(选择表现好的专家),又能探索新的可能性(尝试其他专家)。这于 \(\epsilon_{i,j} \sim \mathcal{N}(0, \sigma(x_i)^2)\) 中的噪声注入机制相呼应,通过在路由器的打分中添加噪声,可以让路由器在训练早期“偶尔换路”,从而更像 bandit 的探索策略。
但是,它显然没有解决Top-K选择的不可微问题,并且,噪声的引入也可能导致训练过程的不稳定:
- 噪声过大:可能导致路由器选择的专家过于随机,每个专家不够专门化,影响模型性能。
- 噪声过小:可能无法有效促进探索,路由器仍然倾向于选择少数几个专家,导致专家崩溃(Expert Collapse)。
课上还提到对 logits做乘法噪声(Multiplicative Perturbation),也是类似的思路,但是也有类似的问题。
2.3.1.3 Auxiliary / Heuristic Balancing Losses
既然MoE训练的难点在于避免专家崩溃(Expert Collapse),那么一个直接的思路就是在主任务损失(Cross Entropy Loss)之外,添加一些辅助损失(Auxiliary Losses)来鼓励专家的均衡使用。这样做的好处是,可以直接引导模型学习更均衡的专家使用策略,从而提升整体性能。在这里,我们介绍两种常用的辅助损失:Load Balancing Loss 和 Z-Loss。
2.3.1.3.1 Load Balancing Loss
Load Balancing Loss 是Switch Transformer(Fedus, Zoph, and Shazeer 2022)中提出的一种辅助损失,旨在鼓励路由器均衡地使用所有专家。具体来说,它通过计算每个专家被选择的频率,并与理想的均衡分布进行比较,从而计算出负载均衡损失。其公式如下: $$
L_{} = N _{i=1}^{N} f_i P_i $${#eq-load-balancing-loss}
其中:
- \(f_i\) 是专家 \(i\) 被选择的频率, 定义为: \[ f_i = \frac{1}{T} \sum_{x \in \mathcal{B}} \mathbb{1} \{\text{argmax } p(x) = i\} \tag{8}\] \(\mathcal{B}\) 是当前批次的样本集合,\(T\) 是token 的数量,\(\mathbb{1}\) 是指示函数,当专家 \(i\) 被选择时取值为1,否则为0。直观来说:expert i 实际上“承担”了多少负载。
- \(P_i\) 是专家 \(i\) 的平均路由概率,定义为: \[ P_i = \frac{1}{T} \sum_{x \in \mathcal{B}} p_i(x) \tag{9}\] 其中,\(p_i(x)\) 是路由器对专家 \(i\) 的输出分数。直观来说:router “本来倾向”把多少概率分给 expert i。
直观来看:如果某个 expert 实际拿了很多 tokens (\(f_i\) 很大),同时 router 还继续给它很高概率(\(P_i\) 很大),那么它的负载均衡损失就会很大,从而促使路由器减少对该专家的选择。反之亦然。
通过最小化负载均衡损失,可以鼓励路由器均衡地使用所有专家,从而提升模型的训练效果。具体来说: - 如果某个专家被选择的次数远高于平均水平,那么它的负载均衡损失就会很大,从而促使路由器减少对该专家的选择。 - 反之,如果某个专家被选择的次数远低于平均水平,那么它的负载均衡损失也会很大,从而促使路由器增加对该专家的选择。
| Deepseek 根据上面的 Load Balancing Loss 设计了一个改进版本。它们提出: |
| - Per-expert Balancing Loss:将上述的负载均衡损失,拓展为Top-K专家的情况。 - Per-Device Balancing Loss:在分布式训练中,考虑每个计算设备上的专家负载均衡。 |
| 我们来看看Per-Device Balancing Loss做的是什么。 我们知道,在分布式训练中,不同的计算设备上可能会有不同数量的专家。如果某个设备上的专家被选择的次数远高于平均水平,那么这个GPU很可能过载,甚至损坏,从而影响整体训练效率。而有些设备上的专家可能几乎没有被选择,导致资源浪费。因此,DeepSeek提出了Per-Device Balancing Loss,旨在鼓励每个计算设备上的专家均衡使用。其公式如下: \[ L_{\text{device}} = \beta \cdot D \cdot \sum_{d=1}^{D} f_d P_d \tag{10}\] |
| 其中: - \(D\) 是计算设备的数量。 - \(f_d\) 是设备 \(d\) 上的专家被选择的频率, - \(P_d\) 是设备 \(d\) 上的专家的平均路由概率。 |
| >Per-expert 保证“专家别死”,Per-device 保证“GPU 别爆”。 |
DeepSeek V3 还提出了另一种改进版本,它们称作Auxiliary Loss Free Balancing,其核心思想是:不再主要依赖 \(\mathcal{L}_{\text{ExpBal}}\) 来做负载均衡,而是通过调整路由器的偏置项(Bias)来实现均衡使用专家。具体来说:
\[ g_{i,j} = \being{cases} s_{i,j} + b_j, \quad s_{i,j} \in \text{Top-K}(s_i) \\ 0, \quad \text{otherwise} \end{cases} \tag{11}\]
直观来看:
- 如果 expert i 最近拿到 token 太小 → 增大\(b_i\) → 它更容易进入 top-K
- 如果 expert i 拿到的 token 太多 → 减小 \(b_i\) → 它更不容易被选中
这是一种在线控制/在线学习式的负载均衡:用规则更新 \(b_i\), 而不是通过梯度下降去学习 \(P_i\)
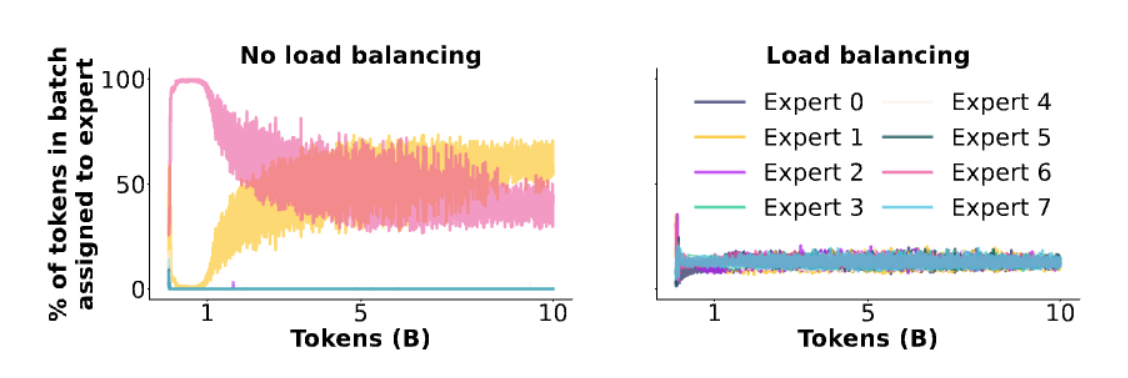
2.3.1.3.2 Z-Loss
Z-Loss 是另一种常用的辅助损失,旨在鼓励路由器的输出分布更加均匀。其公式如下: \[ L_{z} = \sum_{i} \left( \frac{p_i}{\sum_{j} p_j} - \frac{1}{E} \right)^2 \tag{12}\] 其中,\(p_i\) 是路由器对专家 \(i\) 的输出分数,\(E\) 是专家的总数。通过最小化这个损失,可以鼓励路由器的输出分布更加均匀,从而提升模型的训练效果。
2.3.1.4 Loss Combination
在实际应用中,MoE模型的总损失通常由主任务损失(Cross Entropy Loss)和辅助损失(Load Balancing Loss 和 Z-Loss)组成: \[ L_{total} = L_{CE} + \lambda_{load} L_{load} + \lambda_{z} L_{z} \tag{13}\] 其中,\(L_{CE}\) 是主任务损失,\(L_{load}\) 是负载均衡损失,\(L_{z}\) 是Z-Loss,\(\lambda_{load}\) 和 \(\lambda_{z}\)
2.3.2 System Side
在MoE模型的实现中,系统层面的优化也是非常重要的。由于MoE模型通常包含大量的专家,因此在分布式训练中,需要考虑如何高效地管理和调度这些专家,以提升训练效率和模型性能。但是,它们也带来了系统实现上的挑战,比如:
- 每个 token 只激活少数专家(top-K)才能省 FLOPs,但专家往往分散在不同 GPU/节点上,于是训练要频繁做 all-to-all dispatch + all-to-all gather(把 token 发给对应专家算,再收回来合并)。这类通信是否划算取决于专家 FFN 计算是否“够大够重”,能否 amortize 通信成本。
2.3.3 Fine-tuning MoE
MoE fine-tune 更难:更容易不稳定(blow up)+ 更容易过拟合(train–val gap 大)。
2.3.4 Upcycling
MoE 的另一个有趣应用是“Upcycling”(回收利用)。具体来说,先训练好一个 dense Transformer,再把其中的 FFN/MLP 复制成多份专家(experts),加上一个 router,让模型从这一刻起变成 MoE;继续训练一段时间,就能用较低成本得到“总参数更大、推理仍稀疏激活”的 MoE。它解决了“从零训练 MoE 太慢太难”的问题。
3 Others
课程的最后介绍了DeepSeek成功的一些其他技巧,包括:
- Multihead Latent Attention:
- Multi Tokens Prediction
在这里就先不展开介绍了,之后会专门写一篇文章来介绍DeepSeek系列论文的细节。
4 Summary
5 In the End
最后,感谢你一路坚持到这里!创作不易,如果你觉得内容对你有帮助,欢迎请我喝杯咖啡/支付宝红包,支持我继续创作!你们的支持是我最大的动力! :)
