Lecture 15: LLM Alignment SFT & RLHF(PPO, DPO)
在之前的课程中,我们通过训练(Pre-Training)获得了一个可以自动补全的LLM。但是,这个显然和我们现在使用的ChatGPT,Gemini有很大的区别,如何从这个GPT变成ChatGPT,将是我们接下去要学习的内容。也就是所谓的Post-Training,通过Post-Training,模型可以输出制定的内容,并且变得更加安全。在这节Lecture中,我们首先会学习:
- 什么是SFT,如何构建Dataset
- 什么是RLHF
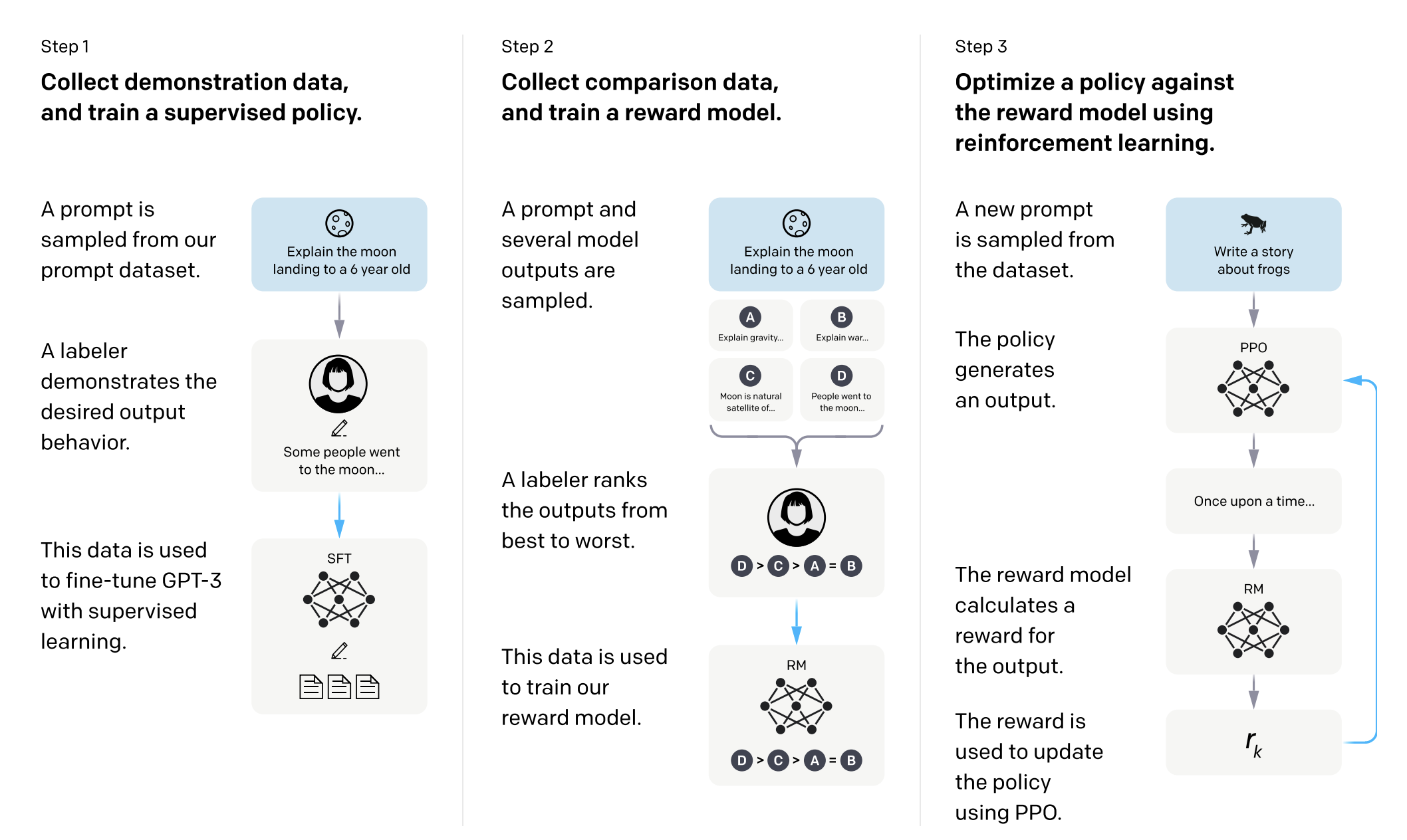
1 SFT
我们知道,训练一个模型,避不开的两件事就是:数据和算法,接下来我们就通过这两个方面来看看SFT
1.1 Dataset
SFT(监督微调)阶段用的数据量通常 远小于预训练,但它对模型行为的影响却极大,所以:
- 数据里的“细节”会被模型强烈放大:风格、长度、格式、口吻、是否爱列点、是否爱加引用、是否爱 emoji……都会被学成“默认行为”。
- SFT 更擅长教会模型输出的“类型签名”(type signature):像不像聊天、是不是有结构、有没有礼貌、会不会拒绝。
- 但 SFT 不一定可靠地教会“新知识”,甚至会引入捷径行为(比如为了符合“专家答案的形式”,去编造引用/事实)。
接下来我们来看看几个SFT数据的例子:
1.1.1 FLAN
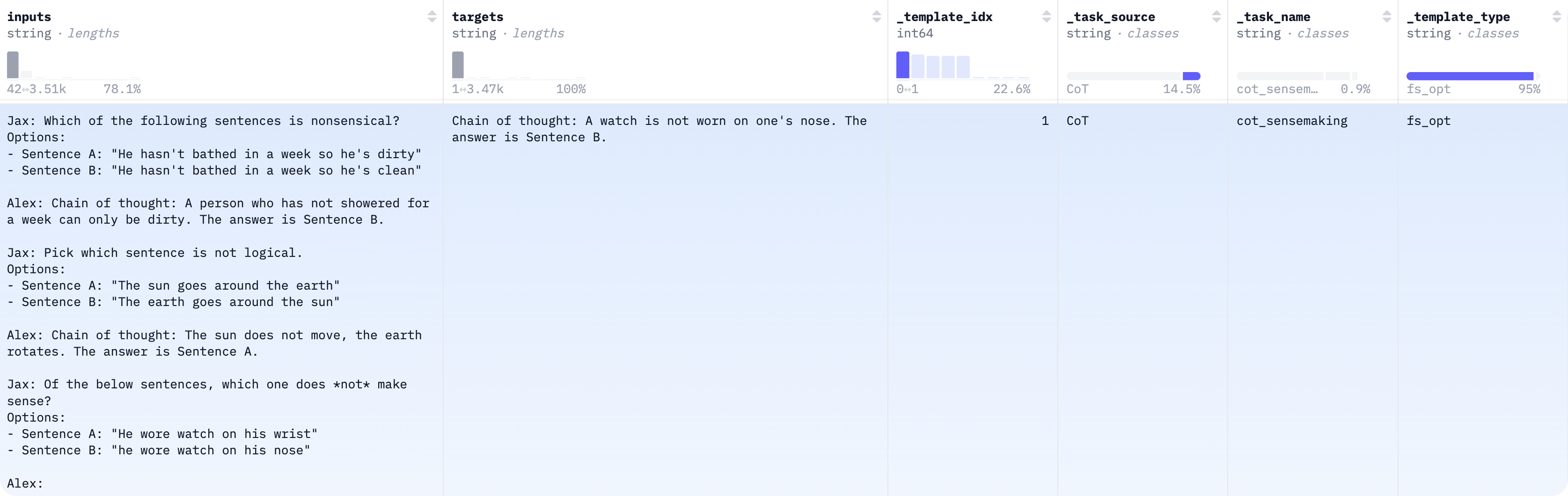
FLAN(Longpre et al. 2023) 数据是把很多 NLP 任务用“自然语言指令模板”表达出来,然后把模型在这些任务上做 instruction tuning(指令微调),从而提升零样本泛化 FLAN 系列的关键不是原始任务,而是: - 把每个任务写成若干种 自然语言模板(instruction + input + output) - 模型训练时看到的是“像聊天指令一样的文本”,但背后很多是分类/抽取/QA/生成等传统任务
论文把它称为 “tasks formatted with instructions” 的 instruction tuning
1.1.2 Alpaca
Alpaca 是斯坦福 CRFM / Tatsu-lab 在 2023 年提出的一个可复现路线:
用 LLaMA-7B 做基座,拿一份由更强模型生成的指令跟随数据(52K)做 SFT,从而得到一个“像 ChatGPT 一样更会听指令”的模型。
它的数据类似于:

下面是Alpaca的Prompt Template
Below is an instruction that describes a task, paired with an input that provides further context. Write a response that appropriately completes the request.
### Instruction:
{instruction}
### Input:
{input}
### Response:通过这种方式,模型学会了“看到 instruction + input 后,应该生成什么样的 response”。
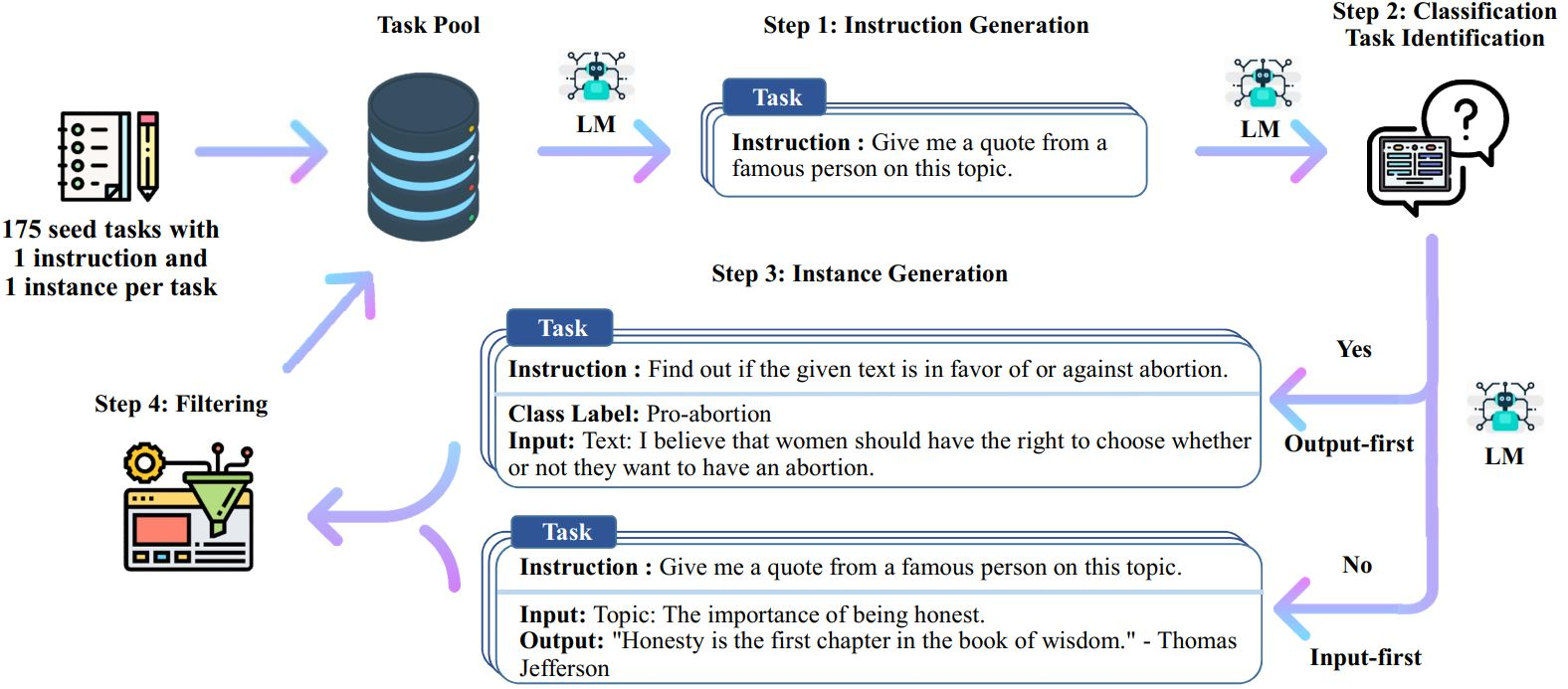
Alpaca 的数据生成基本沿着 Self-Instruct 的思路走:
- 起点:175 条人工写的 seed instruction-output pairs(来自 Self-Instruct 的 seed set)
- 用 text-davinci-003(当时非常强的 teacher):
- 生成更多指令(用 seed 做 in-context 示例,让 teacher 扩写/变换出新 instruction)
- 再让 teacher 为这些指令生成回答,得到“instruction-following demonstrations”
最终形成大约 52K 条数据。
所以 Alpaca 的本质是:用强模型当“数据工厂”,低成本造出大批 instruction→response 的 SFT 样本。
1.1.3 OpenAssistant
OpenAssistant Conversations (OASST1)(Köpf et al. 2023) 是 LAION 组织的全球众包项目产出的一个 “助手风格(assistant-style)对话语料”,目标是把对齐(SFT / RLHF)研究“民主化”:把原本经常被大厂私有化的高质量偏好/对话数据开源出来。它包含 161,443 条消息、35 种语言、超过 10,000 棵完整标注的对话树,并附带大量质量评分。
简要来说,整个数据集由一系列对话树(Conversation Tree, CT)组成。每一棵树的根节点表示一个初始提示(prompt),由“prompter”角色给出;在对话中只区分两种角色:prompter(提问方)和 assistant(回答方),而“user”这个词仅用来指参与数据标注或贡献内容的人类,以避免角色概念混淆。需要注意的是,这两种角色在原则上既可以由人类完成,也可以由模型生成。
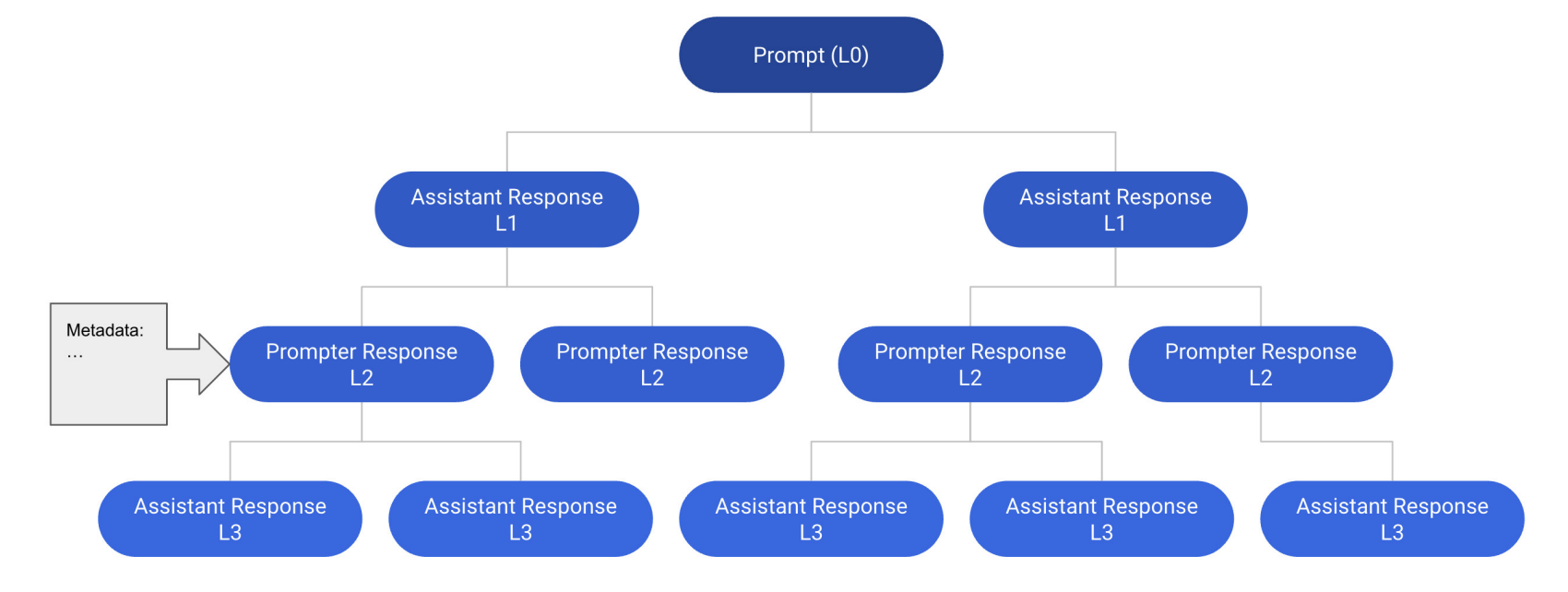
在对话树中: - 每个节点代表一条书面消息,并明确标注其角色(prompter 或 assistant)。 - 每个节点可以有多个子节点,且子节点的角色一定与父节点相反,表示同一轮对话下的不同可能回复。 - 从根节点到树中任意节点的一条路径称为一个 thread,它对应一段合法的完整对话,体现提问方与助手轮流发言的过程。 - 每个节点都会附带额外标注信息,例如人工标签、元数据(采集时间、语言等)。 - assistant 节点还包含排序信息(rank),用于表示在同一父 prompt 下,多条候选回复之间的人类偏好顺序,这是后续偏好学习和奖励建模的重要信号。
整体上,这种对话树结构不仅能表示多轮对话,还能自然地支持一问多答 + 人类偏好排序,非常适合用于指令微调、奖励模型训练以及对齐研究。
下图是OpenAssistant数据集的一个对话树示例:
1.1.4 Self-Annotated Dataset
在课堂上,还一起Label了几个Prompts, 但是从这些Prompts的例子中,明显可以看出有几个问题:
- 质量方差极大(high variance): 同一个 prompt,有人认真写长文、有人一句话、有人直接套 ChatGPT 模板。SFT 会把这种风格差异当成“都对”的示范学进去,导致模型输出风格不稳定。
- “写长、写好”很难 → 数据会偏短或偏模板: 大多数人写不出持续高质量长回答;要么很短,要么用套话填充。模型学到的往往是“模板化结构”,不一定是更有用的内容。
- 容易产生“风格>正确性”的偏置(length/list bias: 人类写作天然倾向于列点、写得更长显得更“像答案”。模型学到的可能是“多写、列点、客气”这种类型签名,而不是“简洁且准确”。
1.2 Algorithm
在了解了SFT的Dataset之后,我们可以训练模型了。其实SFT的算法很简单,与Pre-Training的Object一样,都是Next-Token-Prediction,其基本的代码框架是:token-level NLL)
\[ \underset{\theta}{\max} \log p_{\theta}(y | x) \tag{1}\]
从代码来看,就是简单的几步:
我们可以看到,基本上与Pre-Training的Loss 类似,只不过就是多了一个Response Mask.
Question:为什么要 mask prompt?
因为我们希望模型学的是:“看到 prompt 后,应该怎么答”, 而不是:“把 prompt 也背下来复现一遍”。 通过mask掉 prompt 部分的 loss,我们只让模型在 response 部分学习预测, 并且避免模型过拟合 prompt 内容。
1.2.1 Mid-Training
既然SFT和Pre-Training的训练目标一致,那么我们可不可以将SFT的训练混合到Pre-Training当中呢?答案是可以的,这也就是所谓的Mid-Training/Two-Phase Training
在这个训练过程中,主要做3件事:
- 先正常做预训练(Pre-train on web/pretraining data) 在Common Crawl / books / code / papers 等大规模语料中训练,目标是 next-token prediction。
- 在预训练的后半段,把 instruction-tuning 数据混进去(Mix in instruction-tuning data into pre-training)关键点是:
- 不是等预训练结束再单独 SFT
- 当模型已经有一定能力、学习率开始下降(进入 decay / anneal 阶段)时, 继续用“预训练数据”保持通用能力
- 同时加大“高质量/指令/对话/推理”数据的比例,让模型在还处在“预训练优化状态”时就逐渐学会指令跟随的分布
- 这一步本质上:还是 next-token loss,只是数据分布变了。
- 最后再做一个很短的真正 instruction tuning:由于第二步已经把“指令分布”深度融进模型了,最后的纯 SFT 往往可以更短、更像“校准/收尾”。
通过这个做法的好处就是:让模型能在不严重灾难性遗忘(catastrophic forgetting)的情况下,把 instruction tuning 扩大规模.
我们来对比一下传统 SFT 和 Mid-Training 的区别:
- 传统做法:先预训练完,再 SFT :SFT 数据量虽然小,但梯度信号很集中、风格强,会把模型“拉”到很窄的分布上。
如果你 SFT 过拟合(学习率大/步数多/数据分布太偏),就容易:- 通用能力下降(遗忘预训练里学到的广泛知识/语言能力)
- 过拟合某种风格(更啰嗦、更爱列点、更爱模板化)
- Mid-Training:预训练后期逐步加指令数据 :因为预训练数据还在、学习率也在 decay,模型被“温和地”引导到指令分布,
- 不会一下子被 SFT 的强分布冲刷。
- 同时可以把 instruction 数据规模做大(甚至到“像预训练一样大”),而不用担心彻底把模型训偏。
- 不会一下子被 SFT 的强分布冲刷。
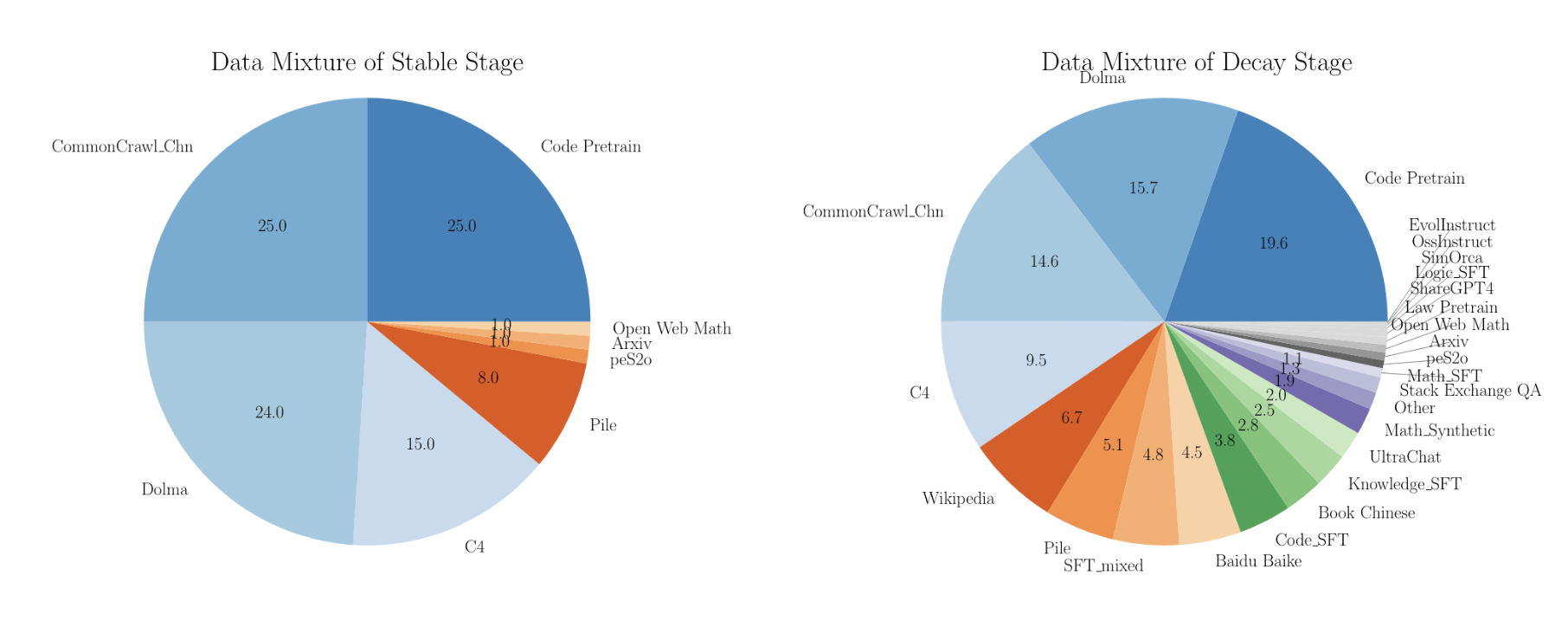
通过这种方法,我们只需要在训练的时候,修改不同阶段的数据比例即可,比如:
- 训练进度前 70%:几乎全是预训练数据
- 后 30%(学习率开始衰减):逐步提高 instruction/高质量数据占比:例如从 0% → 10% → 30% → 50%
- 训练末尾:再做少量纯 SFT(更像“对齐收尾”)
2 RLHF
在前半段,我们学习了SFT,回顾一下SFT,就是你有(prompt, ideal response)示范数据,本质是在做,最大化Next-Token-Prediction的目标 Equation 1。
在强化学习中,这叫也叫做做Imitation Learning。
TIP: What is Imitation Learning?
Imitation Learnings 是通过学习专家示范数据(state/action 或 prompt/response),直接拟合“应该怎么做”,而不是通过试错来优化奖励。简单来说,我们有专家示范数据 \(\mathcal{D} = \{(s_1, a_1), (s_2, a_2), \ldots (s_n, a_n)\}\),目标是最大化: \[ \underset{\theta}{\max} \sum_{(s, a) \in \mathcal{D}} \log \pi_{\theta}(a | s) \]
我们也提到了这种方法存在明显的几个问题,其中包括Dataset的难以收集,偏置会被放大(style/length/list bias)等。因此我们就从SFT(Imitation Learning)走向了Reinforcement Learning(Optimization)。 具体来说,我们把LM当作一个Policy \(\pi_{\theta}( y| x)\), 目标是最大化:
\[ \underset{\theta}{\max} \mathbb{E}_{y \sim \pi_{\theta}( \cdot | x)}[r(x, y)] \tag{2}\]
通过改变我们的训练目标,我们不再需要每个 prompt 的标准答案,而是收集:
- 给同一个 prompt \(x\),模型生成多个回答 \(y_1, y_2\)(rollouts)
- 标注者只做判断:哪个更好(pairwise preference), \(y^+ \succ y^-\)
通过这种训练目标的改变,我们可以节省许多的费用。
并且,这种方法也更符合人类的认知习惯,G-V gap (Generation-Validation gap) 就是一个很好的例子:
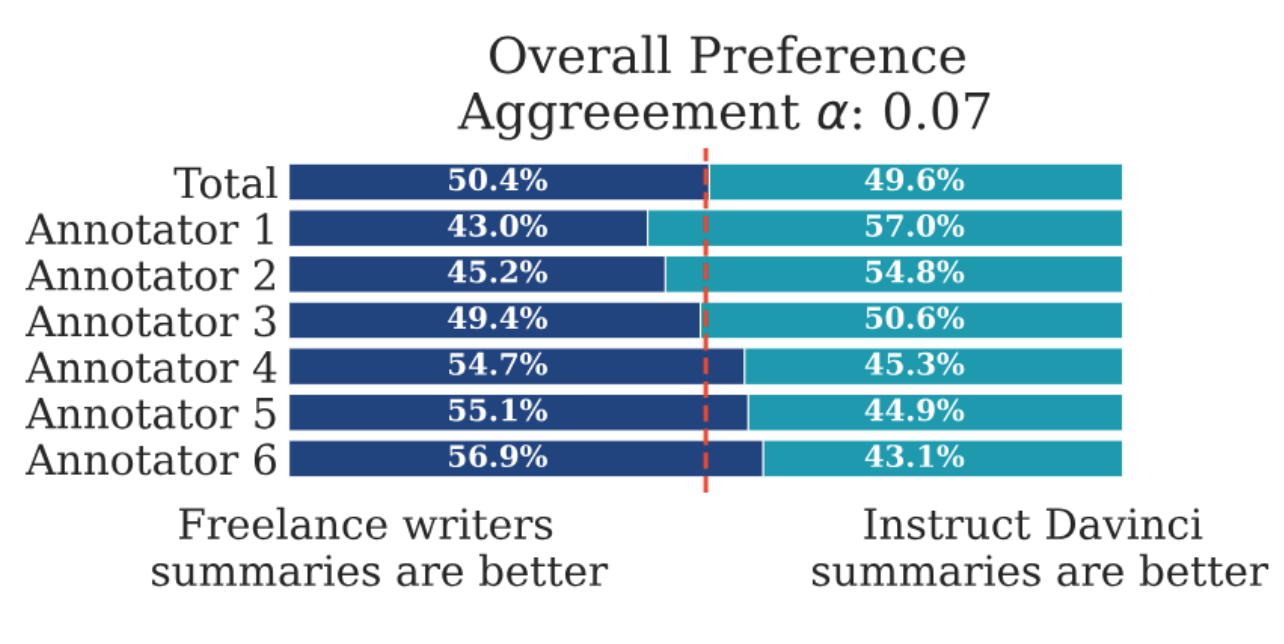
用一句话总结就是: “生成”一个高质量答案很难且不稳定,但“验证/比较”哪个更好相对容易,因此 RLHF 通过偏好比较来优化模型更符合人类真正的偏好。
接下来,我们来具体看看RLHF是个什么东西,与SFT类似,我们主要还是通过两个方面:数据和算法,并且在最后看看RLHF存在什么缺点
2.1 RLHF Data
课上提到 InstructGPT 的标注准则很经典:helpful、truthful、harmless。
实际标注界面通常就是:
- A vs B 哪个更好?(或 4 选 1 / ties 等)
- 有时还会分别打分:事实性、遵循指令、安全性、写作质量等
不过需要注意的是:这不是“对错题”,很多任务是开放式偏好。
有了这些数据之后,我们要训练一个Reward Model \(r_{\phi}(x, y)\). 每个回答都有一个隐藏分数,标注者更常选分高的。
用一个 logistic/softmax 形式拟合:
\[ P(y^+ \succ y^- \mid x) = \sigma\big(r_\phi(x,y^+) - r_\phi(x,y^-)\big) \tag{3}\]
于是你的 RLHF 数据就变成 reward model 的监督数据:
\[ \underset{\phi}{\max} \sum_{(x, y^+, y^-) \in D} \log \sigma\big(r_\phi(x,y^+) - r_\phi(x,y^-)\big) \tag{4}\]
训练完成后,就有了一个 reward model,可以给任意 (x, y) 对打分: \(r_{\phi}(x, y)\)。
当然,这个流程看似简单,实际上还是有很多考量的:
- 数据质量:标注者培训、审核、分布覆盖、偏见控制等
- 数据多样性:prompt 类型、回答风格、难度等
- 模型架构:reward model 通常是一个小型 LM,或者在 LM 上加个头
2.2 RLHF Algorithms
有了Pair-Wise 的Dataset和Reward Model之后,我们可以开始训练的我们的模型了。在InstructGPT(Ouyang et al. 2022) 中,主要用的是PPO的算法。 接下来看看PPO的具体内容。
2.3 PPO
回顾一下,看一下我们现在手头上有些什么东西:
- 一个初始化的策略模型(通常是 SFT 模型)\(\pi_{\text{ref}}(y|x)\)(作为参考策略/基线)
- 一个奖励函数/奖励模型 \(r_{\phi}(x,y)\)(由偏好数据训练出来)
- 要训练的策略 \(\pi_\theta(y|x)\), (由LLM初始化)
RLHF-PPO 的核心目标就是:
\[ \underset{\theta}{\max} \mathcal{J}(\theta) = \mathbb{E}_{y\sim \pi_\theta(\cdot|x)}\big[r_\phi(x,y)\big] \ -\ \beta \, \mathrm{KL}\big(\pi_\theta(\cdot|x)\ \|\ \pi_{\text{ref}}(\cdot|x)\big) \tag{5}\]
通过这个目标函数,我们希望模型: 回答更“高奖励”,但别偏离 SFT 太远(KL 约束防止跑飞、学会作弊或变得怪异/不安全)。
2.3.1 REINFORCE
在Neural Network中,我们优化目标通常用梯度下降法,因此我们需要计算上面目标的梯度。对于Deep RL也不例外,我们需要计算出这个Object Function (Equation 5) 的梯度:
\[ \nabla_\theta \mathbb{E}_{y\sim \pi_\theta(\cdot|x)}\big[r_\phi(x,y)\big] = \mathbb{E}_{y\sim \pi_\theta(\cdot|x)}\left[r_\phi(x,y) \, \nabla_\theta \log \pi_\theta(y|x)\right] \tag{6}\]
通过这个方法,我们可以计算出梯度,然后用SGD来更新模型参数,这也就是REINFORCE算法。 在实际操作中,我们可以通过Sampling的方式来估计上面的期望:
\[ \nabla_\theta \mathbb{E}_{y\sim \pi_\theta(\cdot|x)}\big[r_\phi(x,y)\big] \approx \frac{1}{N} \sum_{i=1}^N r_\phi(x,y_i) \, \nabla_\theta \log \pi_\theta(y_i|x), \quad y_i \sim \pi_\theta(\cdot|x) \tag{7}\]
但是REINFORCE有两个主要问题:
- High variance:奖励信号往往很稀疏且噪声大,导致梯度估计方差很高,训练不稳定。
- 单步更新:REINFORCE 每次更新都基于当前策略采样的数据,不能多步利用旧数据,效率低。
接下来,我们看看如何解决这两个问题,并且逐步引出PPO算法。
2.3.2 Variance Reduction with Advantage Function
我们先来看一下为什么会有High Variance的问题。
假设我们把回答 \(y\) 看成一个序列的动作 \((a_1, a_2, \ldots, a_T)\),每个动作对应生成一个 token。 那么根据链式法则,回答的概率可以写成: \[ \pi_\theta(y|x) = \prod_{t=1}^T \pi_\theta(a_t | s_t) \tag{8}\]
其中 \(s_t\) 是生成第 \(t\) 个 token 时的状态(包括 prompt 和前面生成的 tokens)。 根据 REINFORCE 的梯度公式 Equation 6,我们可以把梯度展开成对每个时间步的贡献求和: \[ \nabla_\theta \mathbb{E}_{y\sim \pi_\theta(\cdot|x)}\big[r_\phi(x,y)\big] = \mathbb{E}_{y\sim \pi_\theta(\cdot|x)}\left[r_\phi(x,y) \sum_{t=1}^T \nabla_\theta \log \pi_\theta(a_t | s_t)\right] \tag{9}\]
这里的关键问题是:奖励 \(r_\phi(x,y)\) 是对整个序列 \(y\) 的评价,但我们把它直接用在每个时间步的梯度上,导致每个时间步的梯度估计都包含了整个序列的噪声,方差很大。
为了降低梯度估计的方差,我们引入优势函数(Advantage Function) \(A_t\),它衡量在状态 \(s_t\) 下采取动作 \(a_t\) 相对于平均水平的好坏:
\[ A_t = Q(s_t, a_t) - V(s_t) \tag{10}\]
其中 \(Q(s_t, a_t)\) 是在状态 \(s_t\) 下采取动作 \(a_t\) 后的预期回报,\(V(s_t)\) 是状态 \(s_t\) 的平均回报。 通过使用优势函数,我们可以把梯度公式改写为: \[ \nabla_\theta \mathbb{E}_{y\sim \pi_\theta(\cdot|x)}\big[r_\phi(x,y)\big] = \mathbb{E}_{y\sim \pi_\theta(\cdot|x)}\left[\sum_{t=1}^T A_t \, \nabla_\theta \log \pi_\theta(a_t | s_t)\right] \tag{11}\]
这样,每个时间步的梯度只受到该时间步优势 \(A_t\) 的影响,减少了整个序列奖励带来的噪声,从而降低了方差。
2.3.3 Off-Policy Updates
REINFORCE 的另一个问题是它是on-policy的:每次更新都需要用当前策略采样新数据,不能多次利用旧数据,效率低。 为了解决这个问题,我们可以采用离线数据重用(off-policy updates)的思想。具体来说,我们可以保存之前采样的数据(prompts 和生成的回答),并在多次迭代中重复使用这些数据进行更新。
但是直接使用旧数据会引入偏差,因为这些数据是根据旧策略 \(\pi_{\theta_{\text{old}}}\) 采样的,而我们现在要更新的是新策略 \(\pi_\theta\)。 为了纠正这种偏差,我们可以使用重要性采样(importance sampling),通过计算每个回答在新旧策略下的概率比来调整梯度估计:
\[ \rho(y) = \frac{\pi_\theta(y|x)}{\pi_{\theta_{\text{old}}}(y|x)} \tag{12}\]
然后,我们可以把梯度公式改写为: \[ \nabla_\theta \mathbb{E}_{y\sim \pi_{\theta_{\text{old}}}(\cdot|x)}\big[r_\phi(x,y)\big] = \mathbb{E}_{y\sim \pi_{\theta_{\text{old}}}(\cdot|x)}\left[\rho(y) \sum_{t=1}^T A_t \, \nabla_\theta \log \pi_\theta(a_t | s_t)\right] \tag{13}\]
这样,我们就可以多次利用旧数据进行更新,提高数据效率。
2.3.4 Proximal Policy Optimization (PPO)
结合上面的两个改进,我们就引出了PPO(Proximal Policy Optimization)算法。PPO 通过限制新旧策略的变化幅度,进一步稳定训练过程。具体来说,PPO 使用一个裁剪目标(clipped objective),防止策略更新过大:
\[ L^{\text{clip}}(\theta) = \mathbb{E}_{y\sim \pi_{\theta_{\text{old}}}(\cdot|x)}\left[\min\left(\rho(y) A, \text{clip}(\rho(y), 1-\epsilon, 1+\epsilon) A\right)\right] \tag{14}\] 其中 \(\epsilon\) 是一个小的超参数,控制裁剪范围(通常是0.1到0.3)。 通过这个裁剪目标,PPO 保证了新策略不会偏离旧策略太远,从而避免了训练不稳定的问题。
我们来看一下PPO的整体训练流程。
- Rollout(采样回答):对一批 prompts \(x\),用当前策略 \(\pi_{\theta_{\text{old}}}\) 生成回答 \(y\)。同时保存每个生成 token 的:
- logprob:\(\log \pi_{\theta_{\text{old}}}(a_t|s_t)\)
- 算奖励(reward):用奖励模型 \(r_{\phi}(x,y)\) 给整段回答一个标量分数。再加上 KL 惩罚,得到最终奖励信号:
KL 惩罚通常有两种做法:
- 显式 KL penalty:把 \(-\beta \, \mathrm{KL}(\pi_\theta(\cdot|x) \| \pi_{\text{ref}}(\cdot|x))\) 加进 reward
- 或在 loss 里单独加 KL 项(类似 InstructGPT)
很多实现把 token-level 的 KL 变成一个 shaping reward:
\[ r_t^{\text{KL}} = -\beta\left(\log \pi_\theta(a_t|s_t)-\log \pi_{\text{ref}}(a_t|s_t)\right) \]
然后把最终奖励分配到序列末端或做一些分摊。
- 估计 Value + Advantage
训练一个 value head \(V_\psi(s_t)\) 预测“从当前前缀往后能拿到的回报”。
用(GAE)等方法得到 \(A_t\)
\[ \delta_t = r_t + \gamma V(s_{t+1}) - V(s_t) = \sum_{l\ge 0}(\gamma\lambda)^l \delta_{t+l} \tag{15}\]
4:PPO update(多 epoch、小步更新)
对同一批 rollout 数据,做 K 个 epoch 的 minibatch 更新:
policy loss:−Lclip-L^{clip}−Lclip
value loss:∥Vψ−R∥2|V_- R|^2∥Vψ−R∥2
entropy bonus:鼓励探索 (+αH)(+H)(+αH)
(可选)KL 控制项
总体 loss(常见形式):
L=Lpolicy+cvLvalue−ceH+cklKLL = L_{} + c_v L_{} - c_e H + c_{kl}L=Lpolicy+cvLvalue−ceH+cklKL
PPO 工程上复杂,主要因为:
on-policy:每轮都要采样新数据(rollouts 成本高)
需要 value function:要训 value head,容易不稳
需要 careful 的 KL 控制:不然要么跑飞、要么学不动
sequence credit assignment:奖励常是序列级,怎么分到 token 上很敏感
长度偏置/奖励 hacking:reward model 可能偏好长回答 → 策略学会“写长骗分”
# PPO RLHF: one training iteration (one "outer step")
# Assumes:
# policy: trainable LM πθ
# ref_policy: frozen LM πref (often SFT checkpoint)
# reward_model: rφ(x, y) -> scalar reward per sequence
# value_head: Vψ(s_t) -> scalar value per token/state (often a head on top of policy)
#
# Notation:
# B = batch size (number of prompts)
# T = max total tokens (prompt + generated)
# Tp = prompt length (varies per sample)
# Tr = response length (varies per sample)
#
# Key masks:
# response_mask[b,t] = 1 if token t is a generated response token (NOT prompt), else 0
# valid_mask[b,t] = 1 if token t exists (not padding), else 0
#
# IMPORTANT alignment:
# For causal LM, token-level logprob at position t corresponds to predicting token_ids[t]
# from prefix token_ids[:t]. Commonly computed with a 1-step shift.
def ppo_train_step(prompts):
# ------------------------------------------------------------
# 1) Rollout: sample responses from current policy (old policy snapshot)
# ------------------------------------------------------------
with no_grad():
policy.eval()
# Generate tokens (can be via vLLM or your sampler)
# returns:
# token_ids: (B, T) padded
# response_mask: (B, T) 1 for response tokens
# valid_mask: (B, T) 1 for non-pad tokens
token_ids, response_mask, valid_mask = generate(policy, prompts)
# (Optional) store prompt lengths, response lengths, etc.
# prompt_mask = valid_mask & (~response_mask)
# Freeze a copy of current params as "old" logically.
# In practice, we keep old_logp computed here as constants.
# ------------------------------------------------------------
# 2) Compute old_logp and ref_logp for the generated response tokens
# ------------------------------------------------------------
with no_grad():
# old policy logprobs on the sampled trajectory
# logp_old: (B, T) where positions not scored can be 0
logp_old = token_logprobs(policy, token_ids) # aligned to token_ids
logp_ref = token_logprobs(ref_policy, token_ids) # aligned to token_ids
# Only optimize on response tokens (typical RLHF)
# Keep only response positions; everything else masked out.
logp_old = logp_old * response_mask
logp_ref = logp_ref * response_mask
# ------------------------------------------------------------
# 3) Reward + KL shaping
# ------------------------------------------------------------
with no_grad():
# Sequence-level reward from reward model (scalar per sample)
# r_seq: (B,)
r_seq = reward_model(prompts, token_ids) # evaluates (x, y)
# Token-level KL term (per token):
# kl_t = logπθ(a_t|s_t) - logπref(a_t|s_t)
# For shaping, we usually use old policy logp here because rollout came from old policy.
# kl_tok: (B, T)
kl_tok = (logp_old - logp_ref) # already masked to response tokens
# KL penalty as "negative reward" per token
# r_kl_tok: (B, T)
r_kl_tok = -beta * kl_tok
# Combine rewards into a token-level reward signal.
# Common simple choice: put the sequence reward at the final response token,
# plus KL penalty at each response token.
# r_tok: (B, T)
r_tok = zeros_like(kl_tok) # (B, T)
last_resp_index = last_index(response_mask) # (B,) gives t_end per sample
r_tok[range(B), last_resp_index] += r_seq # terminal reward
r_tok += r_kl_tok # dense KL shaping
# Ensure padding doesn't contribute
r_tok = r_tok * valid_mask
# ------------------------------------------------------------
# 4) GAE: compute advantages A_t and returns R_t for response tokens
# ------------------------------------------------------------
with no_grad():
# Value predictions for each token/state
# v: (B, T)
v = value_head(policy, token_ids) # or separate critic network
v = v * valid_mask
# Compute next-state values v_next (shifted)
v_next = shift_left(v) # v_next[:, t] = v[:, t+1], last = 0
v_next = v_next * valid_mask
# TD residuals δ_t = r_t + γ v_{t+1} - v_t
# delta: (B, T)
delta = r_tok + gamma * v_next - v
delta = delta * response_mask # only response tokens matter
# GAE recursion backwards over time for each sample
# adv: (B, T)
adv = zeros_like(delta)
gae = zeros(B)
for t in reversed(range(T)):
mask_t = response_mask[:, t] # (B,)
# if mask_t=0, reset gae to 0 so prompt/pad doesn't leak
gae = delta[:, t] + gamma * lam * gae
gae = gae * mask_t
adv[:, t] = gae
# Returns (target for value): R_t = A_t + V_t
ret = adv + v
ret = ret * response_mask
# Normalize advantages over all response tokens in the batch (stabilizes PPO)
adv = masked_normalize(adv, response_mask) # zero-mean, unit-std over masked positions
# ------------------------------------------------------------
# 5) PPO clipped loss (policy + value + entropy)
# ------------------------------------------------------------
policy.train()
# Recompute current policy logprobs for the same token_ids (now θ is trainable)
# logp_new: (B, T)
logp_new = token_logprobs(policy, token_ids)
logp_new = logp_new * response_mask
# Probability ratio ρ_t = exp(logp_new - logp_old)
# ratio: (B, T)
ratio = exp(logp_new - logp_old) * response_mask
# Clipped surrogate objective
# unclipped = ratio * adv
# clipped = clip(ratio, 1-eps, 1+eps) * adv
unclipped = ratio * adv
clipped = clip(ratio, 1 - eps, 1 + eps) * adv
# Policy loss: negative because we maximize objective
# Take masked mean over response tokens
policy_loss = -masked_mean(min(unclipped, clipped), response_mask)
# Value loss: regress to ret (returns)
v_pred = value_head(policy, token_ids) * response_mask
value_loss = masked_mean((v_pred - ret) ** 2, response_mask)
# Entropy bonus (encourage exploration) on response tokens
# entropy_tok: (B, T)
entropy_tok = token_entropy(policy, token_ids) * response_mask
entropy_bonus = masked_mean(entropy_tok, response_mask)
# (Optional) explicit KL term vs ref using current logp_new
# Helps keep policy close even if clip isn't enough
kl_new = (logp_new - logp_ref) * response_mask
kl_mean = masked_mean(kl_new, response_mask)
total_loss = policy_loss + c_v * value_loss - c_ent * entropy_bonus + c_kl * kl_mean
optimizer.zero_grad()
total_loss.backward()
clip_grad_norm_(policy.parameters(), max_grad_norm)
optimizer.step()
# Return logs
return {
"loss_total": total_loss,
"loss_policy": policy_loss,
"loss_value": value_loss,
"entropy": entropy_bonus,
"kl": kl_mean,
"reward_seq_mean": mean(r_seq),
}2.4 DPO
显然,PPO的算法,存在的主要一个缺陷就是所需的内存过多: 我们需要保存:
- Policy: 和LM一样大的模型
- Reference Policy: 和LM一样大的模型
- Value Model: 和LM一样大的模型
- Reward Model: 和LM差不多大的模型
并且,在训练过程中,还需要保存大量的中间激活(activations)用于反向传播(backpropagation)。
这对于动辄几个B的LM模型来说,消耗是巨大的,因此,提出了DPO的算法。 DPO(Direct Preference Optimization)(Rafailov et al. 2024) 可以把“RLHF + PPO”那套 采样→训练reward→RL更新,简化成一个纯监督式的偏好学习:直接用 \((x,y+,y^-)\) 更新策略模型。一句话总结就是: 让模型对 preferred 回答的概率比 rejected 更大,同时用参考模型 πref_{}πref 约束别偏太远。
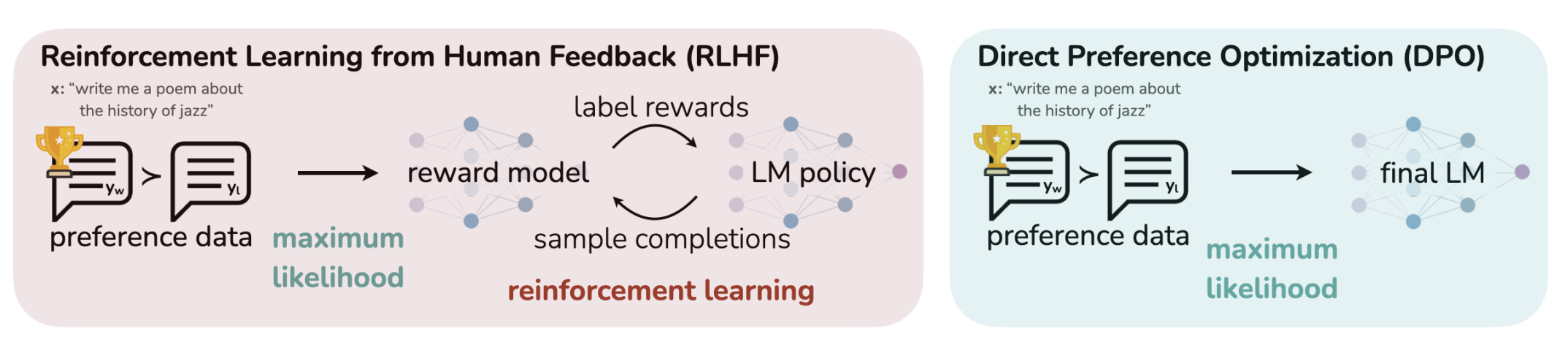
接下来,我们来具体看看DPO算法: 假设 policy 不是神经网络,而是任意分布(nonparametric)。 在这个假设下,这个优化问题有解析解:
πr(y∣x)=1Z(x) πref(y∣x) exp (1βr(x,y))r(y|x)= {}(y|x) !(r(x,y))πr(y∣x)=Z(x)1 πref(y∣x) exp(β1r(x,y))
这其实就是一个 Boltzmann / energy-based reweighting:
参考分布 \(\pi_{\text{ref}}\) 提供“先验”
reward 越高,exp(r/β)(r/)exp(r/β) 越把概率往上推
Z(x)Z(x)Z(x) 是归一化常数(partition function)
2.5 反解”得到 implied reward:reward ≈ log-ratio(差一个常数)
把上式取 log 并整理,得到图里最后一行:
r(x,y)=βlogπr(y∣x)πref(y∣x)+βlogZ(x)r(x,y)= + Z(x)r(x,y)=βlogπref(y∣x)πr(y∣x)+βlogZ(x)
关键点:
βlogZ(x)Z(x)βlogZ(x) 只依赖 x,不依赖 y → 在“比较 y+y^+y+ vs y−y^-y−”时会相消
所以在偏好学习里,你可以把 reward 的差写成:
r(x,y+)−r(x,y−)=β(logπ(y+∣x)πref(y+∣x)−logπ(y−∣x)πref(y−∣x))r(x,y+)-r(x,y-) =( - )r(x,y+)−r(x,y−)=β(logπref(y+∣x)π(y+∣x)−logπref(y−∣x)π(y−∣x))
这一步就是 DPO 的核心:不显式训练 reward model,而是用 policy 的 logprob(相对 ref 的差)来“隐式表示 reward”。
r(x,y+)−r(x,y−)=β[logπref(y+∣x)π(y+∣x)−logπref(y−∣x)π(y−∣x)]
把上面差值写得更紧凑一点:
Δθ(x)=(logπθ(y+∣x)−logπθ(y−∣x))−(logπref(y+∣x)−logπref(y−∣x))(x) =((y+|x)-(y^-|x)) -({}(y+|x)-_{}(y^-|x))Δθ(x)=(logπθ(y+∣x)−logπθ(y−∣x))−(logπref(y+∣x)−logπref(y−∣x))
于是
\[ r(x,y^+) - r(x,y^-) = \beta \, \Delta_\theta(x) \tag{16}\]
代回偏好似然:
LDPO(θ)=−E(x,y+,y−)[logσ(β Δθ(x))]{}() = -{(x,y+,y-)}LDPO(θ)=−E(x,y+,y−)[logσ(βΔθ(x))]
这就是 DPO。
直觉解释:
如果你的新策略 πθ 相比 ref 更偏向 chosen(Δθ 大),loss 小
如果反而更偏向 rejected(Δθ<0_<0Δθ<0),loss 大,会被梯度推回去
在 LLM 里 logπθ(y∣x)_(y|x)logπθ(y∣x) 通常是 response tokens 的 logprob 之和:
logπθ(y∣x)=∑t∈responselogπθ(yt∣x,y<t)(y|x)={t } (y_t x, y{<t})logπθ(y∣x)=t∈response∑logπθ(yt∣x,y<t)
所以 DPO 训练一次 step 就是:
对 batch 中每个样本,分别算:
logp_pos = sum_logp(policy, x, y_pos)logp_neg = sum_logp(policy, x, y_neg)logp_ref_pos = sum_logp(ref, x, y_pos)(no grad)logp_ref_neg = sum_logp(ref, x, y_neg)(no grad)
delta = (logp_pos - logp_neg) - (logp_ref_pos - logp_ref_neg)loss = -log_sigmoid(beta * delta).mean()
import torch
import torch.nn.functional as F
def dpo_train_step(
policy, # trainable LM πθ
ref_policy, # frozen LM πref (e.g., SFT checkpoint)
optimizer,
batch_pos_input_ids, # (B, T) prompt+chosen padded
batch_pos_attn_mask, # (B, T) bool/int
batch_pos_resp_mask, # (B, T) bool: 1 only on response tokens
batch_neg_input_ids, # (B, T) prompt+rejected padded
batch_neg_attn_mask, # (B, T)
batch_neg_resp_mask, # (B, T)
beta: float = 0.1,
max_grad_norm: float | None = 1.0,
):
"""
DPO core update step (ONLY training part).
Assumes inputs are already tokenized + padded and include response masks.
DPO:
delta = (logπθ(y+|x)-logπθ(y-|x)) - (logπref(y+|x)-logπref(y-|x))
loss = -E[ log σ(beta * delta) ]
"""
def seq_logprob(model, input_ids, attn_mask, resp_mask):
# logits: (B, T, V)
logits = model(input_ids=input_ids, attention_mask=attn_mask).logits
# causal shift: logits[:, t] predicts input_ids[:, t+1]
logits = logits[:, :-1, :] # (B, T-1, V)
labels = input_ids[:, 1:] # (B, T-1)
logp = F.log_softmax(logits, dim=-1)
tok_logp = logp.gather(-1, labels.unsqueeze(-1)).squeeze(-1) # (B, T-1)
# align masks with shift
mask = (resp_mask[:, 1:] & attn_mask[:, 1:]).to(tok_logp.dtype) # (B, T-1)
return (tok_logp * mask).sum(dim=-1) # (B,)
# ----- policy logprobs -----
logp_pos = seq_logprob(policy, batch_pos_input_ids, batch_pos_attn_mask, batch_pos_resp_mask)
logp_neg = seq_logprob(policy, batch_neg_input_ids, batch_neg_attn_mask, batch_neg_resp_mask)
# ----- reference logprobs (no grad) -----
with torch.no_grad():
logp_ref_pos = seq_logprob(ref_policy, batch_pos_input_ids, batch_pos_attn_mask, batch_pos_resp_mask)
logp_ref_neg = seq_logprob(ref_policy, batch_neg_input_ids, batch_neg_attn_mask, batch_neg_resp_mask)
# ----- DPO loss -----
delta = (logp_pos - logp_neg) - (logp_ref_pos - logp_ref_neg) # (B,)
loss = -F.logsigmoid(beta * delta).mean()
optimizer.zero_grad(set_to_none=True)
loss.backward()
if max_grad_norm is not None:
torch.nn.utils.clip_grad_norm_(policy.parameters(), max_grad_norm)
optimizer.step()
return {
"loss": float(loss.detach().cpu()),
"delta_mean": float(delta.detach().mean().cpu()),
"pref_acc": float((delta.detach() > 0).float().mean().cpu()),
}2.6 Others
在DPO提出之后,后续也有许多算法对其提出了改进,在这里介绍两种 ### SimPO DPO 的“参考模型项(ref)”可以不要 → 得到 SimPO (no ref) DPO/偏好学习很容易出现:长回答更容易赢
因为 sequence logprob 是 token logprob 的“和”,长度不同会导致比较不公平。
所以把
logπθ(y∣x)=∑t∈ylogpθ(yt∣⋅)(y|x)={ty}p_(y_t|)logπθ(y∣x)=t∈y∑logpθ(yt∣⋅)
改成平均每 token 的 logprob:
1∣y∣logπθ(y∣x)_(y|x)∣y∣1logπθ(y∣x)
图里蓝框就是这个:β/∣yw∣⋅logπθ(yw∣x)/|y_w|(y_w|x)β/∣yw∣⋅logπθ(yw∣x) 和 β/∣yl∣⋅logπθ(yl∣x)/|y_l|(y_l|x)β/∣yl∣⋅logπθ(yl∣x)。
imPO 的 logit 里减了一个 γ:
ΔSimPO=β∣yw∣logπθ(yw∣x)−β∣yl∣logπθ(yl∣x)−γ{} = (y_w|x) - _(y_l|x) -=∣yw∣βlogπθ(yw∣x)−∣yl∣βlogπθ(yl∣x)−γ
直觉:你不是只要 ywy_wyw 比 yly_lyl 好一点点就行,而是希望它至少好过一个幅度(margin)。
γ越大,训练越“严格”。
import torch
import torch.nn.functional as F
def simpo_step(
policy, optimizer,
pos_input_ids, pos_attn, pos_rmask,
neg_input_ids, neg_attn, neg_rmask,
beta: float = 0.1,
gamma: float = 0.0,
):
def seq_logprob_and_len(model, input_ids, attn_mask, resp_mask):
logits = model(input_ids=input_ids, attention_mask=attn_mask).logits
logits = logits[:, :-1, :]
labels = input_ids[:, 1:]
logp = F.log_softmax(logits, dim=-1)
tok_logp = logp.gather(-1, labels.unsqueeze(-1)).squeeze(-1)
mask = (resp_mask[:, 1:] & attn_mask[:, 1:]).to(tok_logp.dtype)
seq_lp = (tok_logp * mask).sum(dim=-1) # (B,)
resp_len = mask.sum(dim=-1).clamp_min(1.0) # (B,)
return seq_lp, resp_len
lp_pos, len_pos = seq_logprob_and_len(policy, pos_input_ids, pos_attn, pos_rmask)
lp_neg, len_neg = seq_logprob_and_len(policy, neg_input_ids, neg_attn, neg_rmask)
# SimPO logit (no ref) + length normalization + margin gamma
delta = (beta * (lp_pos / len_pos) - beta * (lp_neg / len_neg) - gamma)
loss = -F.logsigmoid(delta).mean()
optimizer.zero_grad(set_to_none=True)
loss.backward()
optimizer.step()
return loss2.6.1 Length Normalized DPO
import torch
import torch.nn.functional as F
def dpo_len_norm_step(
policy, ref_policy, optimizer,
pos_input_ids, pos_attn, pos_rmask,
neg_input_ids, neg_attn, neg_rmask,
beta: float = 0.1,
):
def seq_logprob_and_len(model, input_ids, attn_mask, resp_mask):
logits = model(input_ids=input_ids, attention_mask=attn_mask).logits
logits = logits[:, :-1, :]
labels = input_ids[:, 1:]
logp = F.log_softmax(logits, dim=-1)
tok_logp = logp.gather(-1, labels.unsqueeze(-1)).squeeze(-1)
mask = (resp_mask[:, 1:] & attn_mask[:, 1:]).to(tok_logp.dtype)
seq_lp = (tok_logp * mask).sum(dim=-1) # (B,)
resp_len = mask.sum(dim=-1).clamp_min(1.0) # (B,)
return seq_lp, resp_len
# policy
lp_pos, len_pos = seq_logprob_and_len(policy, pos_input_ids, pos_attn, pos_rmask)
lp_neg, len_neg = seq_logprob_and_len(policy, neg_input_ids, neg_attn, neg_rmask)
# ref (no grad)
with torch.no_grad():
lp_ref_pos, len_ref_pos = seq_logprob_and_len(ref_policy, pos_input_ids, pos_attn, pos_rmask)
lp_ref_neg, len_ref_neg = seq_logprob_and_len(ref_policy, neg_input_ids, neg_attn, neg_rmask)
# length-normalized log-ratio
pos_term = (lp_pos / len_pos) - (lp_ref_pos / len_ref_pos)
neg_term = (lp_neg / len_neg) - (lp_ref_neg / len_ref_neg)
delta = beta * (pos_term - neg_term)
loss = -F.logsigmoid(delta).mean()
optimizer.zero_grad(set_to_none=True)
loss.backward()
optimizer.step()
return loss2.7 PPO vs. DPO
PPO 的优势来自“更灵活的优化信号”
PPO 显式做 on-policy rollout + advantage(GAE)+ clip + KL 约束,能更直接地把“奖励模型/偏好信号”转成梯度更新;
DPO/SimPO 更像“把 RL 变成监督学习”,简单、稳定、便宜,但表达能力/可控性有时不如 PPO(尤其当你需要更细的控制或 reward 很复杂时)。右侧 Tülu 3 的表:同一个 benchmark 上,结论也会跟着超参和变体跑
你会看到 SimPO、DPO、PPO、DPO-norm(长度归一化)分数差异不大,而且对 β、γ、学习率、batch size、epoch 很敏感。
⇒ 这页想让你记住:在 RLHF 里,工程细节(数据 + 超参 + 训练recipe)往往比“算法名字”更决定结果。
DPO/SimPO 把 RLHF 简化成“好实现的监督学习”,但 PPO 仍可能在某些数据/奖励/超参组合下更强;因此 RLHF 的实验结论必须连同 setup 一起看。
3 Things to watch out for in RLHF
接下来来我们来看一下RLHF中常见的两个坑:
- 对奖励过度优化(reward overoptimization / reward hacking)
- mode collapse / entropy
3.1 Over-optimization
横轴是 KL distance(RL 后的策略跟初始/参考策略差多远)。
纵轴是 RM score(reward model 给的分)。
曲线先升后“变坏”:一开始往 RM 喜欢的方向走,分数上升;但当 KL 越来越大时,模型会学到 奖励模型的漏洞/捷径,导致:
RM 分数可能还很高,但真实质量(人类偏好/事实性/有用性)开始下降;
这就是典型的 “对代理目标(proxy reward)过拟合”。
一句话:你优化的是 RM,不是人类真实偏好;走太远会开始“刷分”。
3.2 Model Collapse
RLHF 会把模型从“按概率拟合数据”的语言模型,推成“为拿高奖励而输出”的策略模型,从而降低输出分布的熵、压缩多样性,并让模型的置信度不再可信(calibration 变差)。
This is the updated content.
4 Summary
这节课把“后训练(post-training)”的主线串起来了:先用 SFT 把模型从“会续写”拉到“会按指令回答”,再用 RLHF(PPO/DPO/SimPO 等) 去对齐人类偏好与安全规范,并讨论了一个很关键的现实:RLHF 的目标函数本质是“奖励最大化(带 KL 约束)”,这会让模型从概率建模器变成策略优化器,因此会带来需要警惕的副作用——过优化 reward(reward hacking/overfitting)、模式坍缩/熵坍缩(多样性下降),以及更隐蔽但很重要的 calibration 变差(模型给出的概率/置信度不再可靠)。我学到的核心是:对齐不是“再训练一次”这么简单,而是数据、目标、正则、评估共同决定行为;尤其当 reward 有噪声或偏差时,“继续把 reward 拉高”反而会伤害真实质量与泛化,所以必须用 KL、早停、离线评估与多维指标(helpfulness/safety/verbosity/calibration/entropy)去约束与监控。
需要注意的点:第一,SFT 数据很贵且存在 G-V gap(人并不总能写出自己真正偏好的答案),所以偏好数据与奖励学习不可避免;第二,RLHF 的训练信号(pairwise/标量 reward)更容易获取,但也更容易被模型“钻空子”,出现 reward 上升但人评/泛化下降;第三,RLHF 往往会降低熵并破坏校准,这会影响置信门控、工具调用与风险控制等下游系统设计,因此在工程上要把“模型概率”当作策略分数而非可靠置信度,并专门做校准/温度/熵约束与评估。
下一步是 RLVR(Reinforcement Learning with Verifiable Rewards),原因很直接:RLHF 的难点在于“人类偏好”与“奖励模型”都带噪声,标注贵、尺度难、容易过拟合奖励;而 RLVR 把训练信号换成可验证、低噪声、可程序化判定的 reward(例如数学/代码/约束满足/单元测试/格式与可执行检查),让优化目标更接近“客观正确性”,显著降低 reward hacking 的空间,同时成本更低、可扩展性更强。换句话说,RLVR 试图把对齐里最不稳定的一环(主观偏好与代理 reward)替换成更硬的监督信号,从而在规模化训练时更稳、更可控,也更适合把“推理能力”往上拉。