Lecture 03: LM Model Architecture & Hyperparameters
Lecture 03 介绍了现代大模型的核心架构与不同的超参数设计。这节课是理解大模型的基础,内容比较多,建议多看几遍。 本节课的目标是了解下图中的内容:
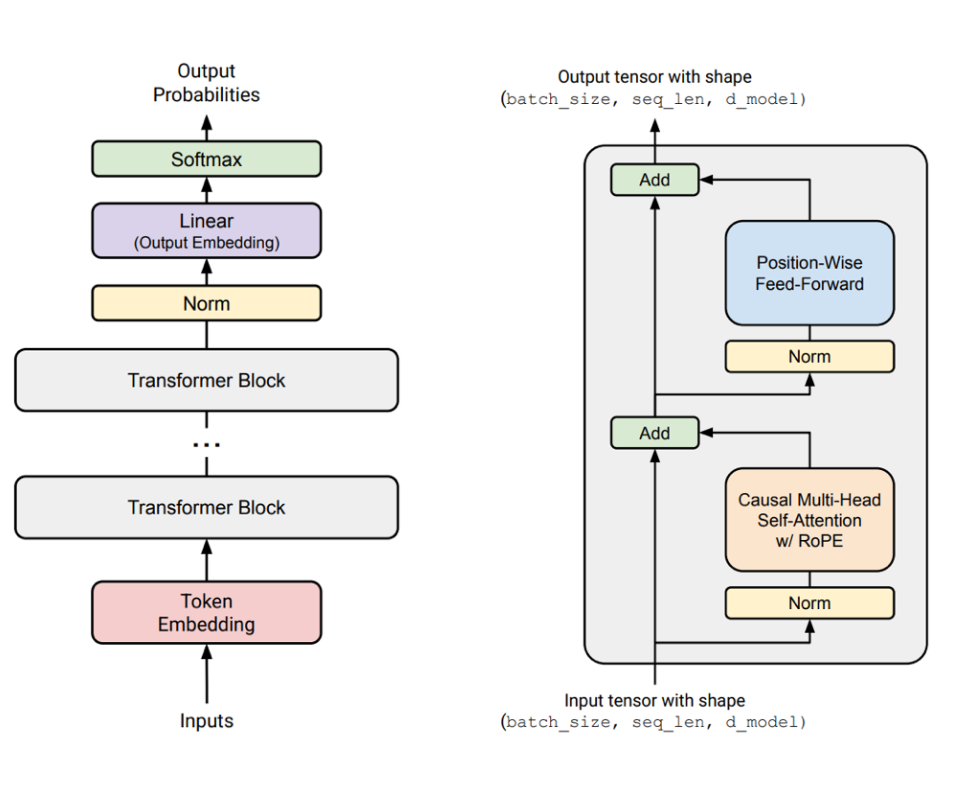
课题的前置条件是理解 Transformer(Vaswani et al. 2023) 模型。 对于那些不理解的同学,可以先学习一下我的这篇文章 100 Paper with Code: Transformer。 在这篇文章中,我详细介绍了 Transformer 的架构与原理,并且配有代码实现,方便大家理解。
1 Transformer 架构回顾
我们先回顾一下 Transformer 的基本架构。 Transformer 由 Vaswani 等人在 2017 年提出(Vaswani et al. 2023),其核心思想是使用自注意力机制来捕捉序列数据中的长距离依赖关系。 Transformer 由 Encoder 和 Decoder 两部分组成,但在大语言模型中,我们通常只使用 Decoder 部分。
Decoder 由多个相同的层堆叠而成,每一层包括以下几个主要组件:
- 位置编码 (Positional Encoding): 用于引入序列中单词的位置信息,因为自注意力机制本身不具备顺序信息。
- 多头自注意力机制 (Multi-Head Self-Attention): 允许模型在不同的表示子空间中关注输入序列的不同部分。
- 前馈神经网络 (Feed-Forward Neural Network): 通常由两个线性变换和一个非线性激活函数组成,用于对每个位置的表示进行进一步处理。
- 残差连接 (Residual Connections): 有助于缓解深层网络中的梯度消失问题。
- 层归一化 (Layer Normalization): 用于稳定训练过程,提高模型的收敛速度。
接下来,我们看看现代大语言模型在 Transformer 基础上做了哪些改进。
2 现代大语言模型架构改进
2.1 Normalization
为什么需要 Normalization?
Normalization 技术在深度学习中起到了稳定训练过程和加速收敛的作用。 它通过调整神经网络层的输入分布,减少了内部协变量偏移 (Internal Covariate Shift),从而使得模型在训练过程中更加稳定。此外,Normalization 还可以帮助缓解梯度消失和梯度爆炸问题,提高模型的泛化能力。
2.1.1 Position of Normalization
2.1.1.1 Post-Norm
在Transformer中,Normalization放置在Sublayer之后,也就是所谓的 Post-Norm 结构。用数学公式表示为:
\[ \text{Post-Norm: } \quad \text{Norm}(x + \text{Sublayer}(x)) \tag{1}\]
然而,(Ba, Kiros, and Hinton 2016) 指出,Post-Norm存在以下的问题:
- 梯度不稳定,特别是在初始化阶段: 论文使用平均场理论分析指出,在 Post-Norm 结构 下(即 LayerNorm 放在残差连接之后),靠近输出层的参数在初始化时梯度期望值很大。 这会导致训练初期梯度爆炸,从而影响模型的稳定性和收敛速度。
- 依赖复杂的 warm-up 超参数调优: 由于 Post-Norm 结构在训练初期容易出现梯度不稳定的问题,因此需要使用复杂的学习率 warm-up 策略来缓解这一问题。 这增加了模型训练的复杂性和调优难度。
Specifically, we prove with mean field theory that at initialization, for the original-designed Post-LN Transformer, which places the layer normalization between the residual blocks, the expected gradients of the parameters near the output layer are large. Therefore, using a large learning rate on those gradients makes the training unstable. The warm-up stage is practically helpful for avoiding this problem. On Layer Normalization in the Transformer Architecture P.1
2.1.1.2 Pre-Norm
为了缓解 Post-Norm 的问题,(Ba, Kiros, and Hinton 2016) 提出了 Pre-Norm 结构,即将 Normalization 放置在 Sublayer 之前。 用数学公式表示为:
\[ \text{Pre-Norm: } \quad x + \text{Sublayer}(\text{Norm}(x)) \tag{2}\]
下图展示了 Post-Norm 与 Pre-Norm 结构的对比:
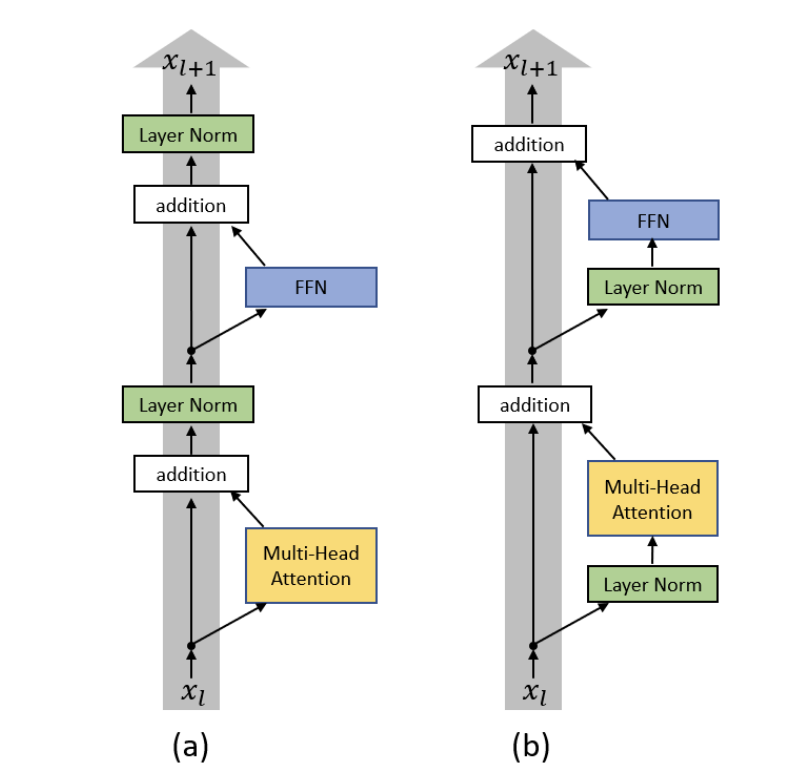
Pre-Norm 有以下优点:
- 提高训练稳定性: Pre-Norm 结构通过在每个子层之前进行归一化,减少了梯度爆炸和梯度消失的风险,从而提高了训练的稳定性。
- 简化超参数调优: 由于 Pre-Norm 结构在训练过程中更加稳定,因此不再需要复杂的学习率 warm-up 策略,简化了模型的训练过程和超参数调优。
We show in our experiments that Pre-LN Transformers without the warm-up stage can reach comparable results with baselines while requiring significantly less training time and hyper-parameter tuning on a wide range of applications. On Layer Normalization in the Transformer Architecture P.1
接下来我们来看一下为什么Pre-Norm能有这么多的好处:
- Gradient Attenuation
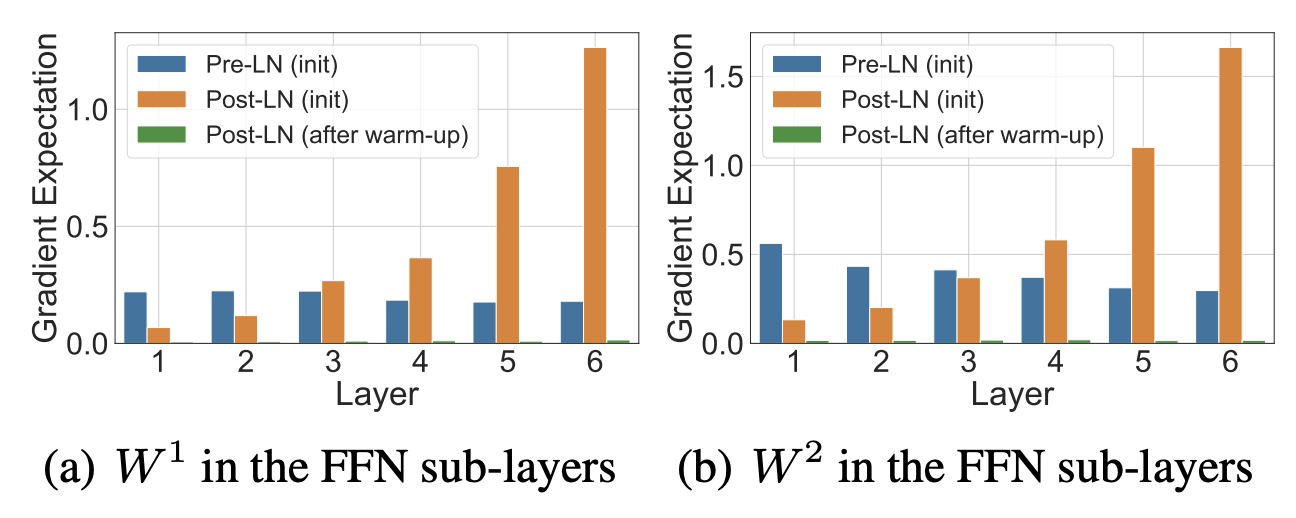
- Gradient Spike / Noise
实验表明 (Nguyen and Salazar 2019)
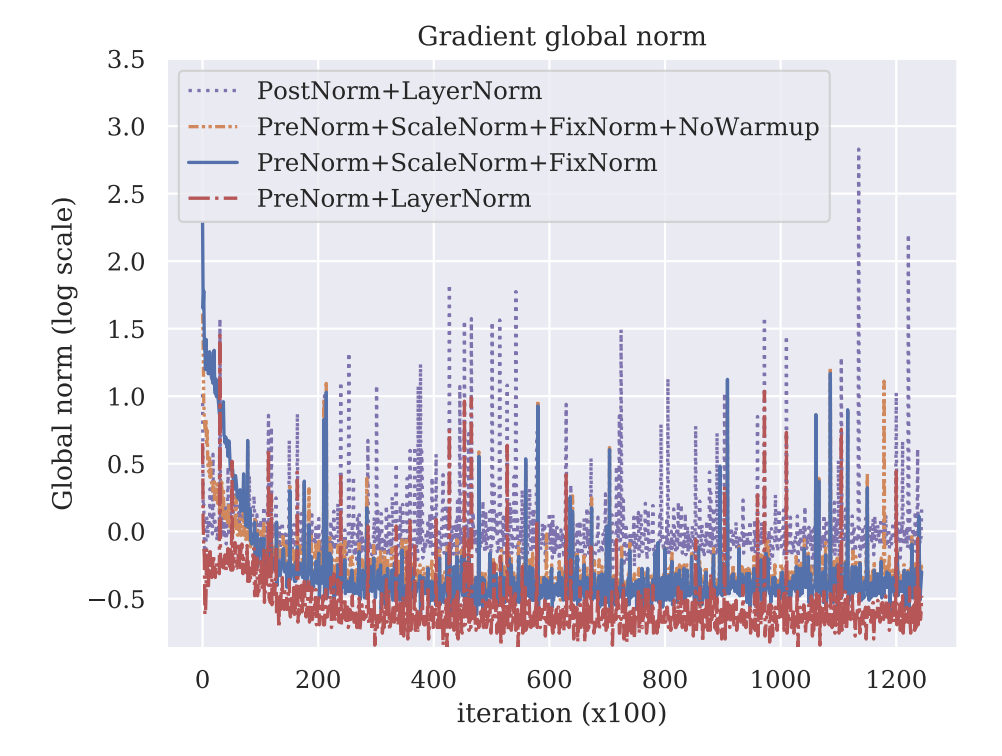
Post-norm produces noisy gradients with many sharp spikes, even towards the end of training. On the other hand, Pre-norm has fewer noisy gradients with smaller sizes, even without warmup. Transformers without Tears: Improving the Normalization of Self-Attention P.6
2.1.1.3 Other Positions
除了 Pre-Norm 和 Post-Norm 之外,还有一些其他的 Normalization 位置设计,例如:
- Sandwich Norm: 将 Normalization 放置在每个子层的输入和输出之间。
- Double Norm: 在每个子层的输入和输出都进行归一化。
从这些实验结果来看,我们可以得出结论: - 尽量保持Residual Connection两端的信号稳定是非常重要的, 这可以保证梯度在网络中顺利传播。
2.1.2 Normalization Types
除了 Normalization 的位置设计之外,Normalization 的形式也是一个重要的设计选择。 常见的 Normalization 形式包括:
- LayerNorm(Ba, Kiros, and Hinton 2016): 对每个样本的特征维度进行归一化,适用于序列数据。
- RMSNorm(RootMeanSquareLayer2020zhang?): 只使用均方根(Root Mean Square)来进行归一化,省略了均值的计算,减少了计算开销。 RMSNorm 在某些情况下可以提供与 LayerNorm 相似的性能,但计算更高效。
原始的Transformer中使用的是LayerNorm, 但是现代大语言模型中,RMSNorm被广泛采用, 例如在 LLaMA(Llama2023touvron?)、GPT-3(LanguageModelsAre2020brown?)、PaLM(ScalingLanguageModels2022chowdhery?) 等模型中都使用了 RMSNorm。
RMSNorm的存在的优势是,
- 计算效率更高: 由于 RMSNorm 省略了均值的计算,因此在计算上更加高效,特别是在大规模模型中,这种效率提升尤为显著。
- 性能相似: 实验表明,在许多任务中,RMSNorm 可以提供与 LayerNorm 相似的性能,尤其是在大语言模型中。
2.2 Activations
Activation Functions给模型引入了非线性,使得神经网络能够学习复杂的函数映射关系。 常见的激活函数包括ReLU、Sigmoid、Tanh等。
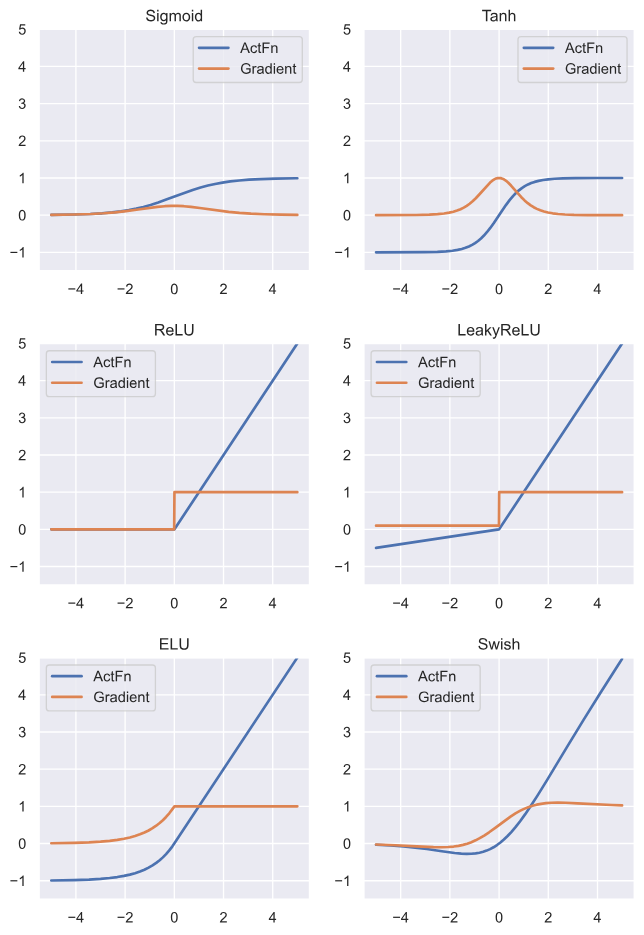
现代LLM中,最常见的激活函数是 Gated Activations家族,例如 SwiGLU,接下来,我们看看这些架构
2.2.1 Gated Activations(*GLU)
Gated Activations 通过引入门控机制,允许模型在前馈神经网络中动态调整信息流,从而提高模型的表达能力和性能。在传统的FFN中,输入通过两个线性变换和一个非线性激活函数进行处理。而在 Gated Activations 中,输入被分成两部分,一部分通过激活函数处理,另一部分通过门控机制进行调节,最终两部分的输出进行元素级乘法操作。用数学公式表示为:
\[ \text{FF} = \textcolor{red}{\max (0, XW_1 )} \ctimes (XW_2 ) \]
Gated Activations 主要改变的就是红色部分,用数学表达就是: \[ \text{Gated FF} = \textcolor{red}{(\max (0, XW_1 ) \odot XV )}W_2 \]
常见的 Gated Activations 包括:
- GeGLU:
\[ \text{GeGLU: } \quad \text{Gated FF} = (\text{GELU}(XW_1 ) \odot XV )W_2 \]
- SwiGLU: \[ \text{SwiGLU: } \quad \text{Gated FF} = (\text{SiLU}(XW_1 ) \odot XV )W_2 \]
实验表明,Gated Activations 在许多任务中都优于传统的激活函数,特别是在大语言模型中,例如 LLaMA(Llama2023touvron?) 和 GPT-4(GPT4TechnicalReport2023openai?) 等模型中都采用了 SwiGLU 作为前馈神经网络的激活函数。
不过需要主要的一点是,Gated Activation引入了一个额外的线性变换矩阵V,这会增加模型的参数量和计算开销。 因此,在实际应用中,为了保持模型数量的不变,通常我们将 \(d_ff\) 设定为 \(\frac{8}{3} d_{model}\), 这样就可以在引入Gated Activation的同时,保持模型的参数量不变。
2.3 Serial & Parallel MLP
传统的Transformer Block是串行的结构 Figure 1, 即先经过Attention模块, 然后再经过MLP模块。 这种设计虽然简单,但在某些情况下可能会限制模型的表达能力。有研究提出了并行的MLP设计,将Attention和MLP模块并行处理,然后将它们的输出进行融合。这种设计可以提高模型的表达能力和计算效率。 用数学公式表示为:
\[ y = x + \text{MLP}(Norm(x)) + \text{Attention}(Norm(x)) \]
通过并行这两层,可以让模型训练的更快速,同时可以减少模型的参数,比如Norm层只需要一层。
不过,目前主流的大语言模型仍然采用串行的Transformer Block设计,但并行的MLP设计为未来的模型架构提供了一个有趣的方向。
2.4 Position Encoding
位置编码 (Positional Encoding) 用于引入序列中单词的位置信息,因为自注意力机制本身不具备顺序信息。 传统的Transformer使用的是绝对位置编码,例如正弦和余弦函数编码(Vaswani et al. 2023)。常见的位置编码方法包括:
- Absolute Position Encoding: 使用固定的编码方式为每个位置分配一个唯一的向量表示。
- Relative Position Encoding(SelfAttentionWithRelative2021shaw?): 通过计算单词之间的相对位置来引入位置信息,增强模型对序列中单词相对关系的理解能力。
- Rotary Position Embedding (RoPE)(RoFormerEnhancedTransformer2021su?): 通过旋转位置向量来引入位置信息,增强模型对长距离依赖关系的捕捉能力。
接下来我们重点介绍 RoPE。
2.4.1 Rotary Position Embedding (RoPE)
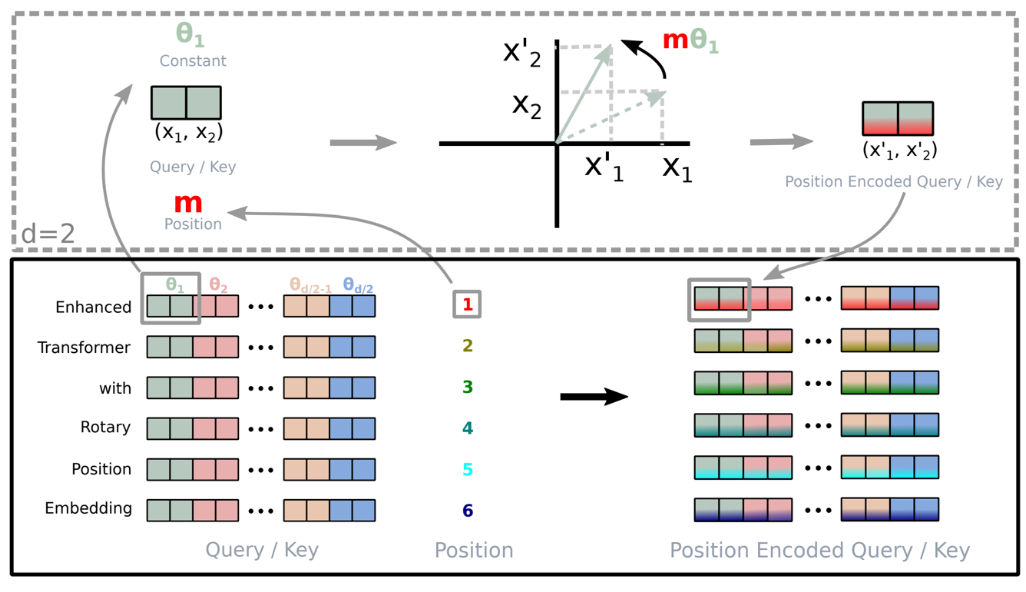
RoPE 通过对查询和键的向量进行旋转来引入位置信息。 具体来说,RoPE 将位置编码表示为一个旋转矩阵,然后将查询和键的向量与该旋转矩阵相乘,从而引入位置信息。 用数学公式表示为:
\[ \text{RoPE}(Q, K, P) = (Q R(P), K R(P)) \] 其中,\(R(P)\) 是位置编码对应的旋转矩阵。
用数学表示就是: \[ R_{\Theta,m}^{d} \mathbf{x} = \begin{pmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_{d-1}\\ x_d \end{pmatrix} \otimes \begin{pmatrix} \cos(m\theta_{1})\\ \cos(m\theta_{1})\\ \cos(m\theta_{2})\\ \cos(m\theta_{2})\\ \vdots\\ \cos\!\big(m\theta_{d/2}\big)\\ \cos\!\big(m\theta_{d/2}\big) \end{pmatrix} + \begin{pmatrix} - x_2\\ x_1\\ - x_4\\ x_3\\ \vdots\\ - x_d\\ x_{d-1} \end{pmatrix} \otimes \begin{pmatrix} \sin(m\theta_{1})\\ \sin(m\theta_{1})\\ \sin(m\theta_{2})\\ \sin(m\theta_{2})\\ \vdots\\ \sin\!\big(m\theta_{d/2}\big)\\ \sin\!\big(m\theta_{d/2}\big) \end{pmatrix} \]
我非常推荐以下的视频,它很清楚的介绍了RoPE以及它的扩展,有兴趣的同学可以前去查看:
3 Hyper-Parameters
训练神经网络就像是炼丹,超参数的选择对于模型的性能有着至关重要的影响。 以下是一些常见的超参数及其选择原则:
3.1 MLP Width
MLP的宽度通常设置为模型维度的4倍,例如对于一个512维的模型,MLP的宽度通常设置为2048。 这种设计可以提供足够的表达能力,同时不会过度增加计算开销。 当然,我们在之前提到过, 如果使用Gated Activation, 那么MLP的宽度通常设置为 \(\frac{8}{3}\) 倍的模型维度。基本上目前主流的大语言模型都是采用这个比例。
除了Gated Activation之外, 也有一些模型使用更宽的MLP, 例如 T5 使用了 64 倍的MLP宽度, 但是这种设计会显著增加计算开销, 因此需要权衡模型性能与计算资源。
至于为什么选择4倍或者 \(\frac{8}{3}\) 倍的MLP宽度, 主要是基于经验和实验结果。 研究表明,这些比例可以在保持模型性能的同时,提供足够的表达能力。
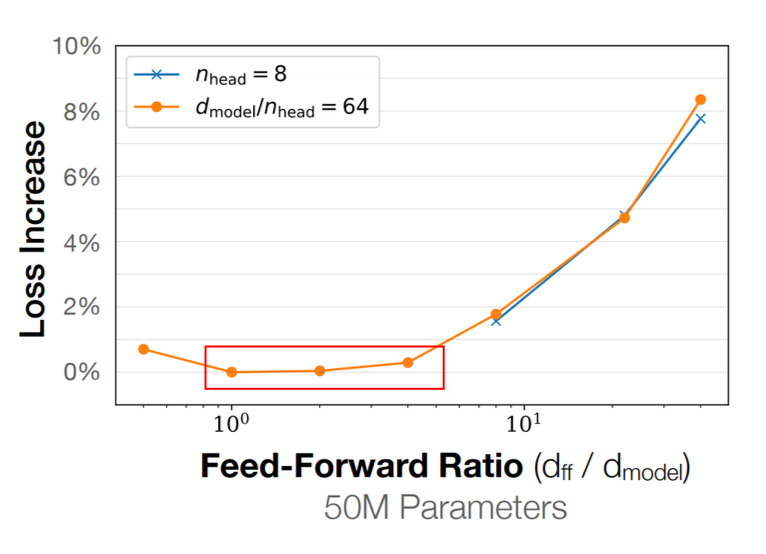
3.2 Attention Heads
模型的Head Dim 通常设置为 d_model / num_heads, 也就是说,Head Dim 与模型维度成反比。 常见的Head Dim设置包括64、128等。不过,Head Dim 不一定就是d_model / num_heads。 不过并没有实验表明,Head Dim 过大或者过小会显著影响模型性能。 因此,在实际应用中,通常根据计算资源和模型规模来选择Head Dim。
3.3 Aspect Ratio
Aspect Ratio 指的是模型的深度(n_layer)与宽度(d_model)之比。 研究表明,较高的Aspect Ratio(即更深的模型)通常可以提供更好的性能,特别是在处理复杂任务时。 然而,过深的模型也可能导致训练困难和过拟合问题。
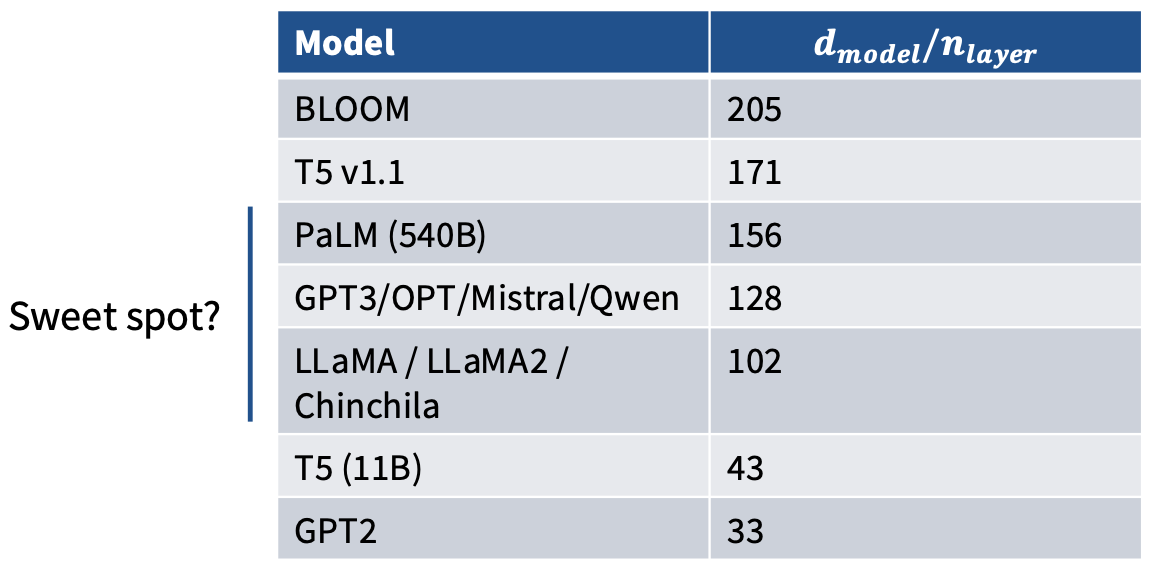
不过过深的模型也会带来一些挑战,例如Parallelism和训练稳定性问题。 因此,在选择Aspect Ratio时,需要权衡模型性能与训练稳定性。
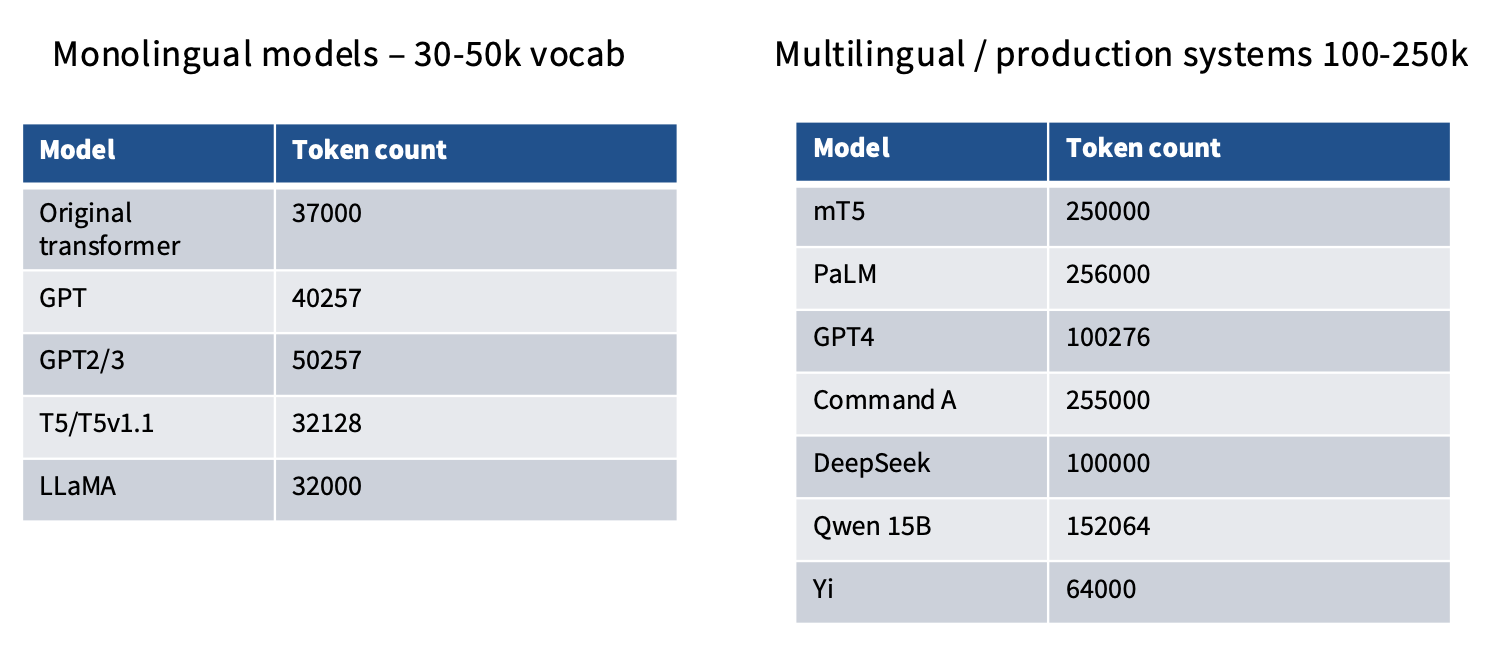
3.4 Vocabulary Size
词表大小(Vocabulary Size)是指模型在训练和推理过程中使用的唯一单词或子词的数量。 词表大小的选择对于模型的性能和计算效率有着重要影响。对于单一个语言的模型,常见的词表大小范围在30,000到100,000之间。 对于多语言模型,词表大小通常更大,以覆盖更多的语言和词汇。
3.5 Regularization
正则化技术用于防止模型过拟合,提高模型的泛化能力。但是许多人提出了一个问题, 大模型是否还需要正则化? 当模型足够大时, 它们似乎并不容易过拟合, 因此正则化的必要性受到质疑。
4 Stability Tricks
在训练大语言模型时,稳定性是一个重要的考虑因素。
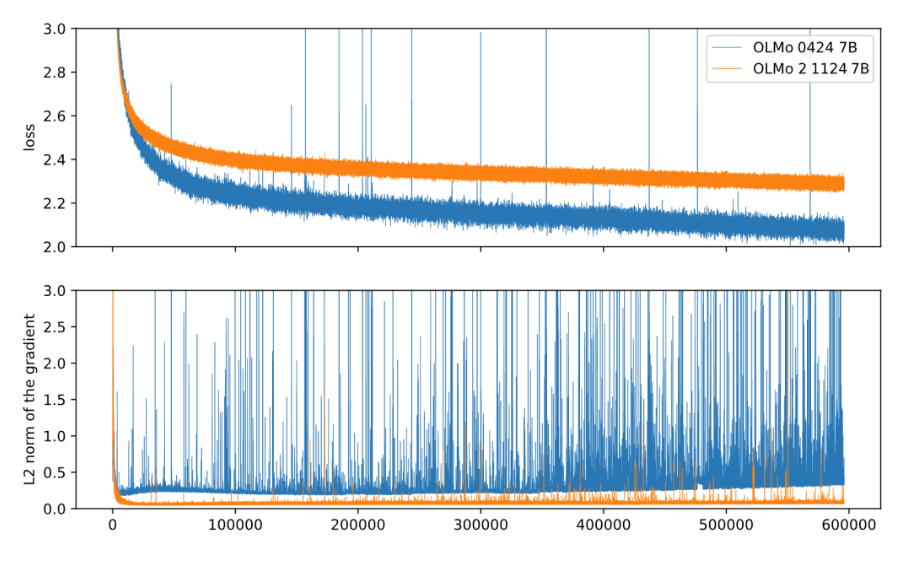
我们希望Loss 曲线尽可能的平滑, 类似于橙色曲线,而不希望出现剧烈的波动, 类似于蓝色曲线。 为了实现这一目标, 研究人员提出了一些稳定性技巧。不过我们先来看看为什么会出现不稳定的情况。
其中一个主要原因是由于注意力机制中的点积操作。 在计算注意力权重时,查询和键的点积可能会导致数值过大或过小,并且将这些值传递给Softmax函数时,可能导致值的极端分布,从而引发训练不稳定。
在这种情况下,很自然的想到对点积结果进行归一化处理,从而缓解数值不稳定的问题。 下面我们介绍几种常见的稳定性技巧。
- QK-Norm: 对查询和键进行归一化处理,确保它们的范数为1,从而稳定点积结果。 用数学公式表示为:
- Logit-soft-capping: 对注意力权重的对数进行截断,防止极端值影响Softmax计算。
- z-loss: 在计算交叉熵损失时,添加一个正则化项,鼓励模型输出的logits保持在一个合理的范围内,从而提高训练稳定性。
5 Attentions
Attention 机制是 Transformer 的核心组件之一。 在大语言模型中,注意力机制的设计对于模型的性能和计算效率有着重要影响。 下面介绍几种常见的注意力机制设计:
5.1 Grouped Query Attention (GQA) / Multi-Query Attention (MQA)
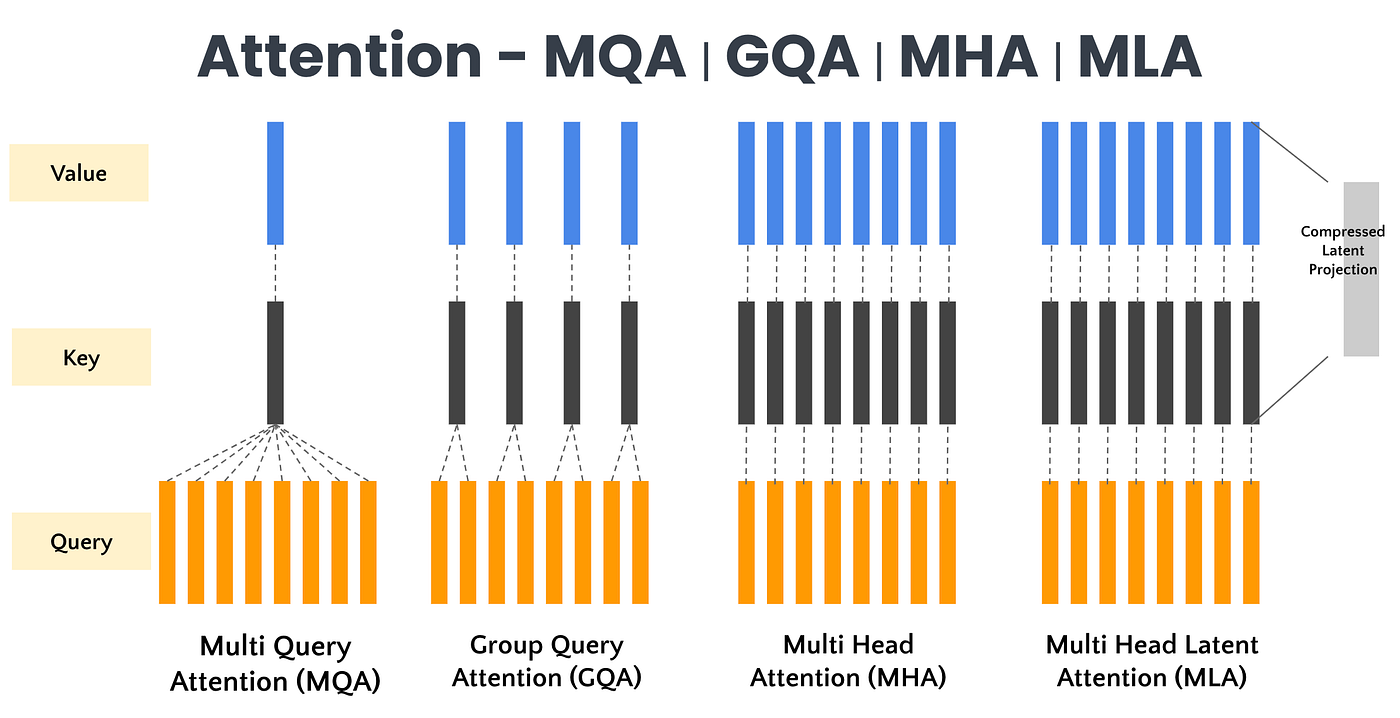
5.2 Sparse / Sliding Window Attention
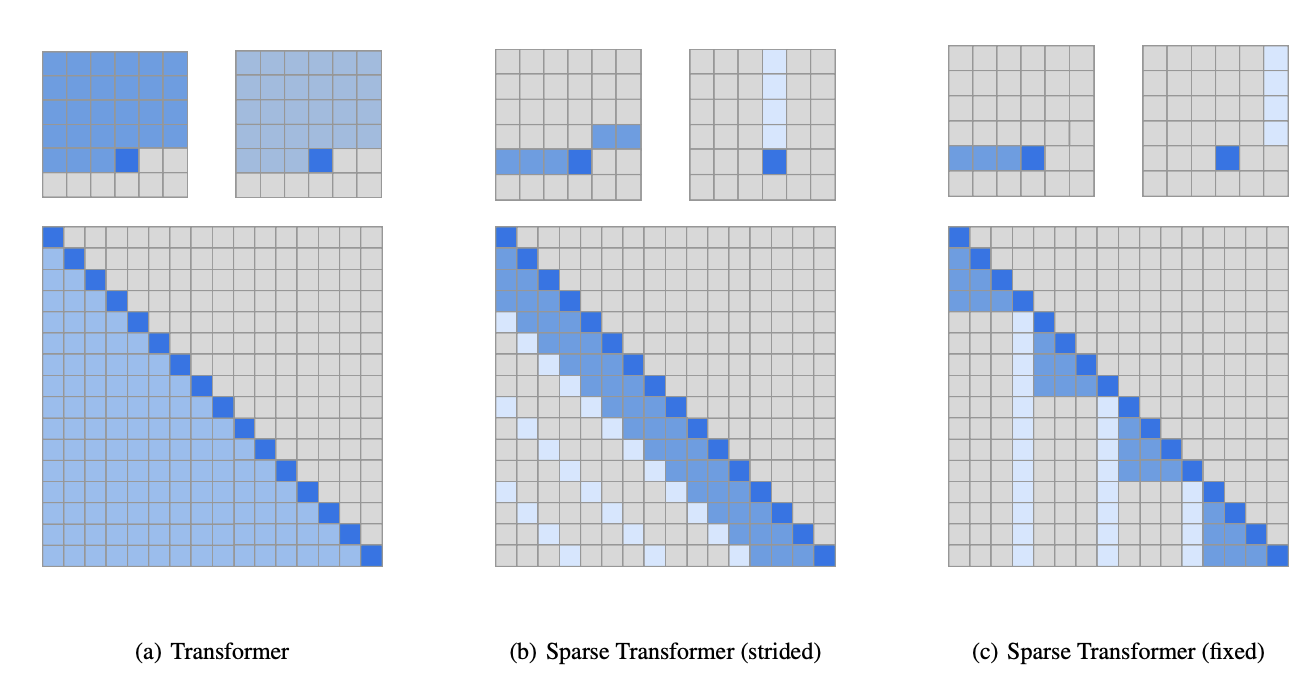
Child et al. (2019)
5.3 Sliding Window Attention
5.4 Interleaved Attention
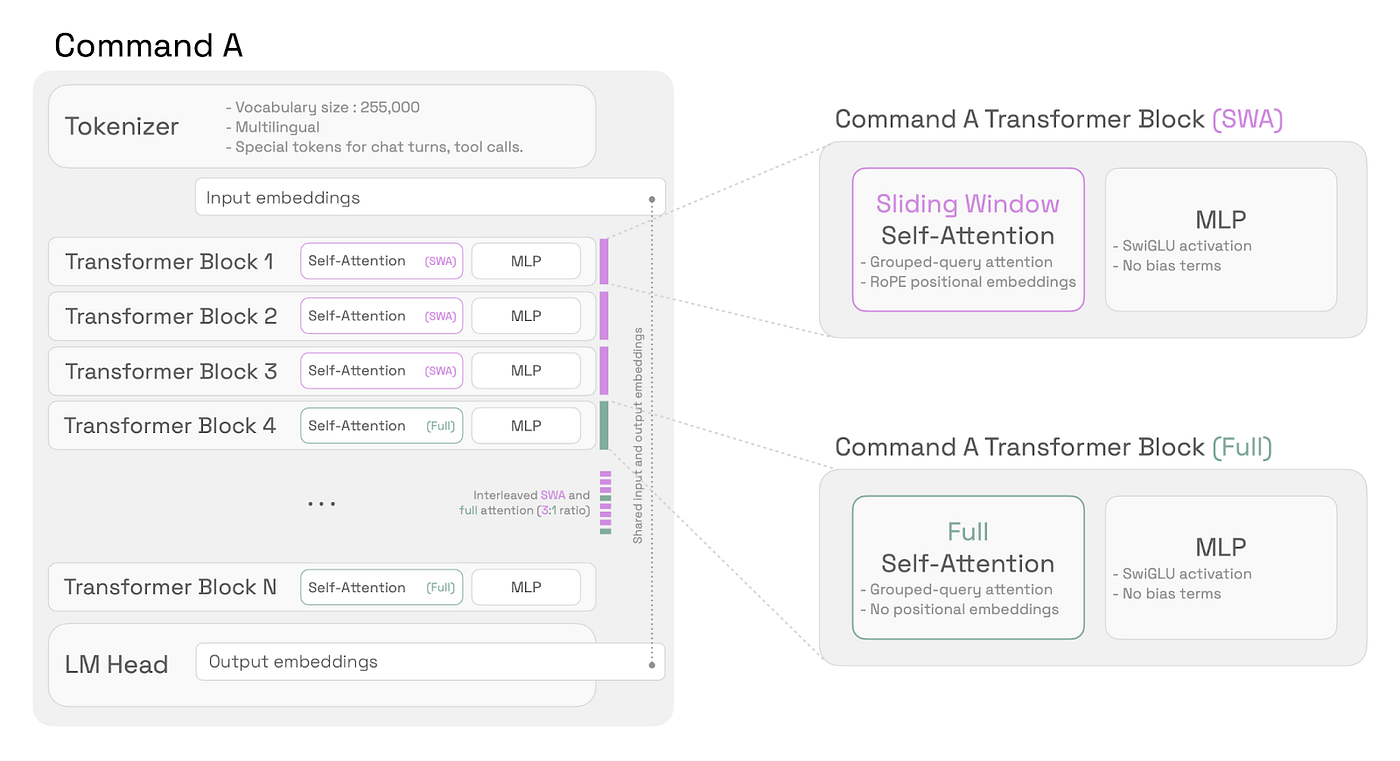
6 Summary
这节课的信息量还是比较大的,建议大家多看几遍,主要的就是全面的介绍了现代大语言模型的架构设计与超参数选择原则。 理解这些内容对于后续学习大模型的训练与优化非常重要。 这节课就是简单的介绍了现代LLM的基础选择,由于时间原因, 许多内容都没有深入展开, 比如稳定性技巧, 以及各种Attention的设计。 后续我会专门写一些文章来介绍这些内容, 大家可以持续关注我的博客。
完成了这三节Lecture之后,我们可以实现 Assignment 1了, 大家可以参考我的代码实现: CS336-Assignment1